Все формулы объема геометрических тел
Все формулы объема геометрических телВсе формулы объема геометрических тел
a — сторона куба
Формула объема куба, (V ):
a, b, c— стороны параллелепипеда
Формула объема параллелепипеда, (V):
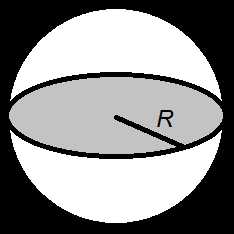
R— радиус шара
π ≈ 3,14
Объем шара, (V):
h— высота шарового слоя
R— радиус нижнего основания
r— радиус верхнего основания
π ≈ 3,14
Объем шарового слоя, (V):
h — высота сегмента
R — радиус шара
π ≈ 3,14
Объем шарового сектора, (V):
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R — радиус шара
h — высота сегмента
π ≈ 3,14
Объем шарового сегмента, (V):
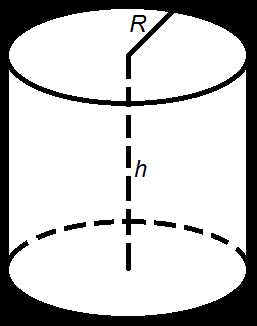
h— высота цилиндра
r— радиус основания
π ≈ 3,14
Объем цилиндра, (V):
H- высота конуса
R- радиус основания
π ≈ 3,14
Объем конуса, (V):
R- радиус нижнего основания
r- радиус верхнего основания
h- высота конуса
π ≈ 3,14
Объем усеченного конуса, (V ):
h — высота пирамиды
S — площадь основания ABCDE
Объем пирамиды, (
h — высота пирамиды
Sниж — площадь нижнего основания, ABCDE
Sверх — площадь верхнего основания, abcde
Объем усеченной пирамиды, (V):
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Объем правильной пирамиды, (V):
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
h — высота пирамиды
a — сторона основания
Объем правильной треугольной пирамиды, (V):
h — высота пирамиды
a — сторона основания
Объем правильной четырехугольной пирамиды, (V):
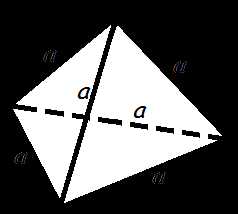
Правильный тетраэдр- пирамида у которой все грани, равносторонние треугольники.
а -ребро тетраэдра
Объем правильного тетраэдра (
© 2016 Все права защищены.
При использовании материалов сайта ссылка на источник обязательна.
zdesformula.ru
Формулы для вычисления массы тел различной формы
9.05.2013 // Владимир ТруновЭто странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
Формулы объема геометрических фигур.
Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объем куба

Объем куба равен кубу длины его грани.
Формула объема куба
где
V
— объем куба,a
— длина грани куба.Объем призмы
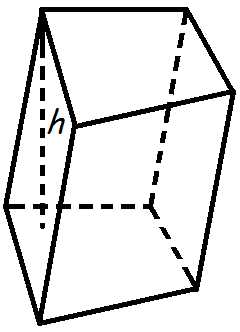
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы
где
V
— объем призмы,So
— площадь основания призмы,h
— высота призмы.Объем параллелепипеда
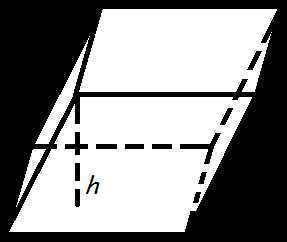
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
где
V
— объем параллелепипеда,So
— площадь основания,h
— длина высоты.Объем прямоугольного параллелепипеда
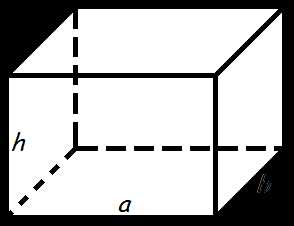
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
где
V
— объем прямоугольного параллелепипеда,a
— длина,b
— ширина,h
— высота.Объем пирамиды
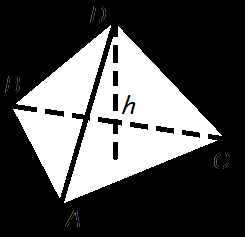
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды
где
V
— объем пирамиды,So
— площадь основания пирамиды,h
— длина высоты пирамиды.Объем правильного тетраэдра
Формула объема правильного тетраэдра
где
V
— объем правильного тетраэдра,a
— длина ребра правильного тетраэдра.Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
- Формулы объема цилиндра
- V =
π R
2h
- V =
So h
V
— объем цилиндра,So
— площадь основания цилиндра,R
— радиус цилиндра,h
— высота цилиндра,π = 3.141592
.Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса
где
V
— объем конуса,So
— площадь основания конуса,R
— радиус основания конуса,h
— высота конуса,π = 3.141592
.Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Формула объема шара
где
V
— объем шара,R
— радиус шара,π = 3.141592
.Добавить комментарий
o-math.com
| Главная > Учебные материалы > Математика: Формулы площадей и объемов геометрических фигур | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Формулы площадей 1.Площадь многоугольника. Формулы объемов1.Объем куба.2.Объем параллелепипеда. 3.Объем призмы. 4.Объем пирамиды. 5.Объем усеченной пирамиды. 6.Объем цилиндра. 7.Объем правильной треугольной пирамиды. 8.Объем конуса. 9.Объем усеченного конуса. 10.Объем тетраэдра. 11.Объем шара. 12.Объем шарового сегмента и сектора. Примеры решений С1. Видео. |
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
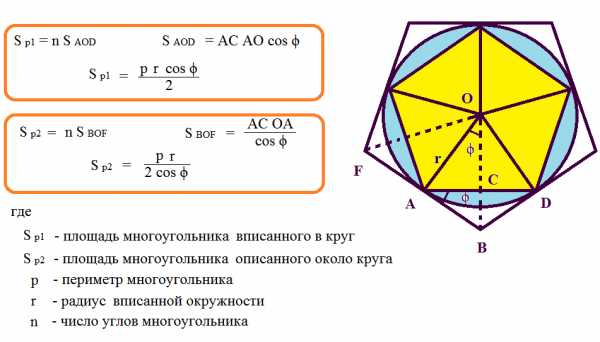
Площадь многоугольника |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
Рассчитать площадь многоугольника вписанного в круг и описанного около круга |
|||||||||||||||||||||||||
Площадь треугольника |
|||||||||||||||||||||||||
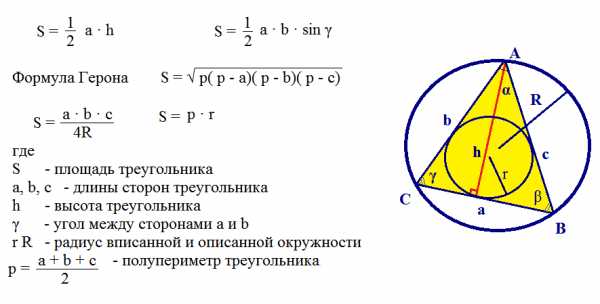 |
|||||||||||||||||||||||||
Рассчитать площадь треугольника |
|||||||||||||||||||||||||
Площадь квадрата |
|||||||||||||||||||||||||
Рассчитать площадь квадрата |
|||||||||||||||||||||||||
Площадь прямоугольника |
|||||||||||||||||||||||||
Рассчитать площадь прямоугольника |
|||||||||||||||||||||||||
Площадь параллелограмма |
|||||||||||||||||||||||||
Рассчитать площадь параллелограмма |
|||||||||||||||||||||||||
Площадь ромба |
|||||||||||||||||||||||||
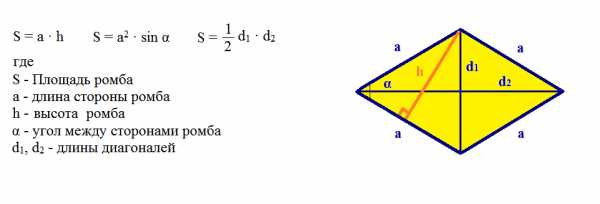 |
|||||||||||||||||||||||||
Рассчитать площадь ромба |
|||||||||||||||||||||||||
Площадь трапеции |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
Рассчитать площадь трапеции |
|||||||||||||||||||||||||
Площадь четырехугольника |
|||||||||||||||||||||||||
Рассчитать площадь четырехугольника |
|||||||||||||||||||||||||
Площадь круга |
|||||||||||||||||||||||||
Рассчитать площадь круга, длину окружности |
|||||||||||||||||||||||||
Площадь кругового сектора, длина дуги |
|||||||||||||||||||||||||
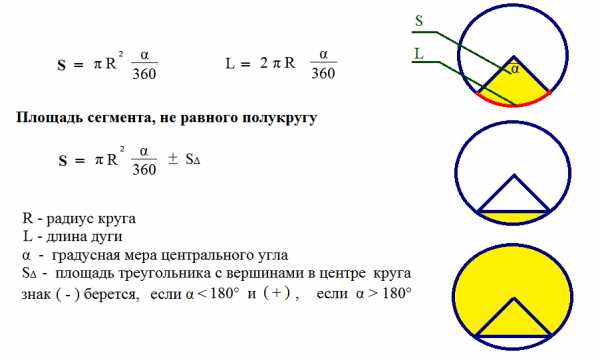 |
|||||||||||||||||||||||||
Рассчитать площадь кругового сектора, длину дуги |
|||||||||||||||||||||||||
Площадь эллипса |
|||||||||||||||||||||||||
Рассчитать площадь эллипса |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Объем куба |
|||||||||||||||||||||||||
Рассчитать объем и площадь поверхности куба |
|||||||||||||||||||||||||
Объем параллелепипеда |
|||||||||||||||||||||||||
Рассчитать объем параллелепипеда |
|||||||||||||||||||||||||
Объем призмы |
|||||||||||||||||||||||||
Рассчитать объем призмы |
|||||||||||||||||||||||||
Объем пирамиды |
|||||||||||||||||||||||||
Рассчитать объем пирамиды |
|||||||||||||||||||||||||
Объем усеченной пирамиды |
|||||||||||||||||||||||||
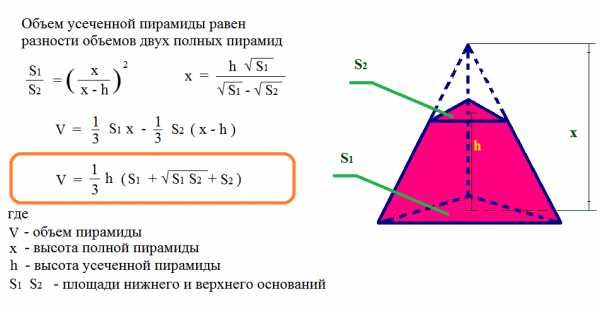 |
|||||||||||||||||||||||||
Рассчитать объем усеченной пирамиды |
|||||||||||||||||||||||||
Объем цилиндра |
|||||||||||||||||||||||||
Рассчитать объем цилиндра |
|||||||||||||||||||||||||
Объем правильной треугольной пирамиды |
|||||||||||||||||||||||||
Рассчитать объем правильной треугольной пирамиды |
|||||||||||||||||||||||||
Объем конуса |
|||||||||||||||||||||||||
Рассчитать объем конуса |
|||||||||||||||||||||||||
Объем усеченного конуса |
|||||||||||||||||||||||||
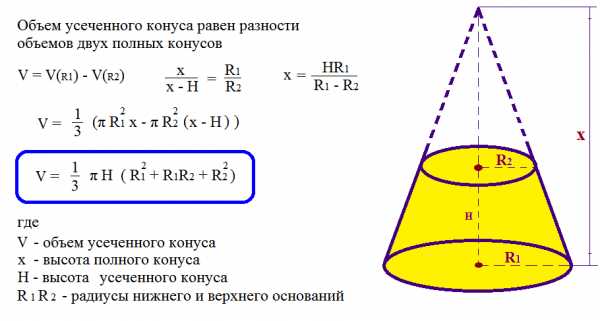 |
|||||||||||||||||||||||||
Рассчитать объем усеченного конуса |
|||||||||||||||||||||||||
Объем тетраэдра |
|||||||||||||||||||||||||
Рассчитать объем тетраэдра |
|||||||||||||||||||||||||
Объем шара |
|||||||||||||||||||||||||
Рассчитать объем и площадь поверхности шара |
|||||||||||||||||||||||||
Объем шарового сегмента и сектора |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
Рассчитать объем шарового сегмента |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
www.mathtask.ru
Объем, Площадь поверхности, формулы объема
Стандартное обозначение объема есть V.
Этим мы измеряем количество (наример, воды), которая может заполнить фигуру.
Только пространственные фигуры имеют объем. Например, треугольники, квадраты не имеют объема, но шар имеет объем (потому что он может быть заполнен чем-то, например водой).
Прямоугольный параллелепипед
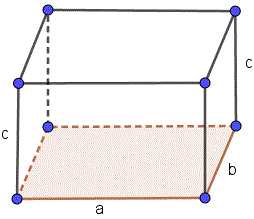
Прямоугольный параллелепипед это фигура, все стороны которой — прямоугольники.
Если длины стороны прямоугольника в основе есть a и
b и третье ребро c
тогда формула объема есть:
$V = a \cdot b \cdot c$
Площадь поверхности:S = $2(a \cdot b + a \cdot c + b \cdot c)$
Куб
Куб есть параллелепипедом, все ребра (стороны) которого равны.

Если длина стороны куба равна a, тогда формула объема:
$V = a.a.a = a^3$
Площадь поверхности:$S = 6a \cdot a = 6a^2$
Параллелепипед
Параллелепипед это фигура, все стороны которой — параллелограммы.
Если площадь основы равна S и высота параллелепипеда равны h,
то формула объема есть:
$V = S \cdot h$
Пирамида
Пирамида это фигура, основа которой есть треугольник, параллелограмм (квадрат, прямоугольник) или другая фигура с n-углами и треугольными сторонами.
Если площадь основы есть S и высота пирамиды есть h,
тогда формула ее объема есть:
$V = \frac{1}{3} \cdot S \cdot h$
Правильный тетраэдр
$V = \frac{\sqrt{2}\cdot a^3}{12}$
Площадь поверхности:$S = \sqrt{3}\cdot a^2$
Конус
Конус это фигура с основанием в виде окружности и имеющая одну вершину, как у пирамиды.
Если площадь основы есть S и длиныа стороны конуса равна h,
то формула объема есть:
$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$
Площадь поверхности(прямого кругового конуса):$S=\pi\cdot r(r + l)$
Сфера
Сфера есть шар.
Она имеет радиус — расстояние от центральной точки сферы к поверхности. Если длина радиуса есть R,
то формула объема есть:
$V = \frac{4}{3} \cdot \pi \cdot r^3$
Площадь поверхности:$S = 4\cdot\pi\cdot r^2$
Цилиндр
Цилиндр это фигура с двумя параллельными окружностями.
Если ралиус основы равен r и высота (расстояние между основами) цилиндра есть h,
то его объем вычисляется по формуле:
$V = \pi \cdot r^2 \cdot h$
Площадь поверхности прямого кругового цилиндра(на картинке):$S = 2\cdot\pi\cdot r(h + r)$
www.math10.com
Как рассчитать объем бревна?

Бревна очень часто используются для постройки домов из сруба, бань, беседок и других построек. Для того, чтобы закупить или заготовить правильное количество материала необходимо узнать его объем. Итак, как же рассчитать объем бревна?
Объем бревна измеряют в кубических метрах и называют кубатура бревна.
Необходимо знать объем бруса как при строительстве, так и при продаже- покупке дров.
Рассмотрим, как посчитать кубатуру круглого леса.
Существует несколько способов, которые широко используются для того, чтобы определить объем круглого леса.
Как определить объем бревна. Способ 1
этот метод заключается в измерении объема пространства в котором находятся бревна. Это может быть склад, сарай, поленница, кузов фуры и другие строения прямоугольной формы. Для того, чтобы определить объем бревна в помещении необходимо:
— измерить кубический объем пространства. Для этого измерьте высоту, и ширину помещения. Полученные значения нужно умножить друг на друга. Получение значение и есть объем.
— важно учитывать, что бревна, сложенные в помещении, не занимают все его пространство, между бревнами образуются прослойки воздуха, такие прослойки необходимо исключить из общего объема. Считается, что такие прослойки занимают примерно 20% пространства. Соответственно, восемьдесят процентов занимает древесина. Коэффициент пустот, который используют в формуле, составляет 0,8. Для того, чтобы рассчитать объем бруса необходимо умножить объем помещения на коэффициент пустот (0,8). Полученная цифра и будет кубатурой бревна.
Как определить объем бревна — способ 2

Второй метод расчета кубатуры бревна подходит для бруса одинаковой длинны и примерно одинакового диаметра.
Рассчитать объем бревна формула:
v = Pi*R*L,
Pi — 3,14
R — радиус бревна
L — длинна бревна
Так как бревна имеют похожий диаметр, но все же немного отличаются для более точного результата нам необходимо замерить какой объем занимают три бревна. Вычисляем мы это по формуле, приведенной выше. После этого три полученных значения суммируем и делим на три, таким образом мы получим усредненное значение объема. Это значение умножаем на количество бревен, таким образом мы получим число обозначающее объем всего пиломатериала.
Как определить объем бруса способ 3

Третий способ часто используют в строительстве для того что бы определить какой объем бревна необходим для постройки того или иного здания. Представляет собой он готовые таблицы, в которых уже приведены посчитанные значения объема, наработанные строителями. Для того, чтобы найти необходимое значение вам потребуется замерить диаметр и длину имеющегося у вас бревна и подставить полученные значения в таблицу, на пересечении вы получите объем бревна.
Кубатура бревна таблица:
| Диаметр, см / Длина, м | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 |
| 10 | 0,026 | 0,031 | 0,037 | 0,044 | 0,051 | 0,058 | 0,065 | 0,075 | 0,082 | 0,09 | 0,1 |
| 11 | 0,032 | 0,037 | 0,045 | 0,053 | 0,062 | 0,07 | 0,08 | 0,09 | 0,098 | 0,108 | 0,12 |
| 12 | 0,038 | 0,046 | 0,053 | 0,063 | 0,073 | 0,083 | 0,093 | 0,103 | 0,114 | 0,125 | 0,138 |
| 13 | 0,045 | 0,053 | 0,062 | 0,074 | 0,085 | 0,097 | 0,108 | 0,12 | 0,132 | 0,144 | 0,158 |
| 14 | 0,052 | 0,061 | 0,073 | 0,084 | 0,097 | 0,11 | 0,123 | 0,135 | 0,15 | 0,164 | 0,179 |
| 15 | 0,06 | 0,071 | 0,084 | 0,097 | 0,11 | 0,125 | 0,139 | 0,153 | 0,169 | 0,182 | 0,199 |
| 16 | 0,069 | 0,082 | 0,095 | 0,11 | 0,124 | 0,14 | 0,155 | 0,172 | 0,189 | 0,2 | 0,22 |
| 17 | 0,077 | 0,092 | 0,107 | 0,124 | 0,14 | 0,157 | 0,174 | 0,191 | 0,209 | 0,225 | 0,25 |
| 18 | 0,086 | 0,103 | 0,12 | 0,138 | 0,156 | 0,175 | 0,194 | 0,21 | 0,23 | 0,25 | 0,28 |
| 19 | 0,097 | 0,115 | 0,134 | 0,154 | 0,173 | 0,193 | 0,212 | 0,235 | 0,255 | 0,275 | 0,305 |
| 20 | 0,107 | 0,126 | 0,147 | 0,17 | 0,19 | 0,21 | 0,23 | 0,26 | 0,28 | 0,3 | 0,33 |
| 21 | 0,119 | 0,14 | 0,163 | 0,185 | 0,21 | 0,23 | 0,255 | 0,285 | 0,31 | 0,335 | 0,365 |
| 22 | 0,13 | 0,154 | 0,178 | 0,2 | 0,23 | 0,25 | 0,28 | 0,31 | 0,34 | 0,37 | 0,4 |
| 23 | 0,144 | 0,169 | 0,194 | 0,22 | 0,25 | 0,275 | 0,305 | 0,335 | 0,37 | 0,4 | 0,435 |
| 24 | 0,157 | 0,184 | 0,21 | 0,24 | 0,27 | 0,3 | 0,33 | 0,36 | 0,4 | 0,43 | 0,47 |
| 25 | 0,171 | 0,197 | 0,23 | 0,26 | 0,295 | 0,325 | 0,36 | 0,395 | 0,43 | 0,465 | 0,505 |
| 26 | 0,185 | 0,21 | 0,25 | 0,28 | 0,32 | 0,35 | 0,39 | 0,43 | 0,46 | 0,5 | 0,54 |
| 27 | 0,203 | 0,23 | 0,27 | 0,305 | 0,345 | 0,38 | 0,42 | 0,46 | 0,495 | 0,54 | 0,585 |
| 28 | 0,22 | 0,25 | 0,29 | 0,33 | 0,37 | 0,41 | 0,45 | 0,49 | 0,53 | 0,58 | 0,63 |
| 29 | 0,235 | 0,27 | 0,31 | 0,355 | 0,395 | 0,44 | 0,485 | 0,525 | 0,57 | 0,62 | 0,675 |
| 30 | 0,25 | 0,29 | 0,33 | 0,38 | 0,42 | 0,47 | 0,52 | 0,56 | 0,61 | 0,66 | 0,72 |
| 31 | 0,265 | 0,31 | 0,355 | 0,405 | 0,45 | 0,5 | 0,555 | 0,6 | 0,655 | 0,71 | 0,77 |
| 32 | 0,28 | 0,33 | 0,38 | 0,43 | 0,48 | 0,53 | 0,59 | 0,64 | 0,7 | 0,76 | 0,82 |
| 33 | 0,3 | 0,35 | 0,405 | 0,46 | 0,51 | 0,565 | 0,625 | 0,68 | 0,74 | 0,805 | 0,87 |
| 34 | 0,32 | 0,37 | 0,43 | 0,49 | 0,54 | 0,6 | 0,66 | 0,72 | 0,78 | 0,85 | 0,92 |
| 35 | 0,34 | 0,395 | 0,455 | 0,515 | 0,57 | 0,635 | 0,7 | 0,76 | 0,83 | 0,9 | 0,97 |
| 36 | 0,36 | 0,42 | 0,48 | 0,54 | 0,6 | 0,67 | 0,74 | 0,8 | 0,88 | 0,95 | 1,02 |
| 37 | 0,375 | 0,44 | 0,505 | 0,57 | 0,635 | 0,705 | 0,78 | 0,85 | 0,925 | 1 | 1,075 |
| 38 | 0,39 | 0,46 | 0,53 | 0,6 | 0,67 | 0,74 | 0,82 | 0,9 | 0,97 | 1,05 | 1,13 |
| 39 | 0,41 | 0,48 | 0,555 | 0,63 | 0,705 | 0,78 | 0,86 | 0,945 | 1,02 | 1,105 | 1,19 |
| 40 | 0,43 | 0,5 | 0,58 | 0,66 | 0,74 | 0,82 | 0,9 | 0,99 | 1,07 | 1,16 | 1,25 |
| 41 | 0,45 | 0,53 | 0,61 | 0,695 | 0,775 | 0,86 | 0,95 | 1,035 | 1,125 | 1,22 | 1,315 |
| 42 | 0,47 | 0,56 | 0,64 | 0,73 | 0,81 | 0,9 | 1 | 1,08 | 1,18 | 1,28 | 1,38 |
| 43 | 0,495 | 0,585 | 0,67 | 0,765 | 0,85 | 0,945 | 1,045 | 1,14 | 1,24 | 1,34 | 1,445 |
| 44 | 0,515 | 0,61 | 0,7 | 0,8 | 0,89 | 0,99 | 1,09 | 1,2 | 1,3 | 1,4 | 1,51 |
| 45 | 0,543 | 0,64 | 0,735 | 0,835 | 0,935 | 1,035 | 1,14 | 1,25 | 1,355 | 1,465 | 1,58 |
| 46 | 0,57 | 0,67 | 0,77 | 0,87 | 0,98 | 1,08 | 1,19 | 1,3 | 1,41 | 1,53 | 1,65 |
| 47 | 0,595 | 0,7 | 0,805 | 0,91 | 1,02 | 1,13 | 1,245 | 1,355 | 1,475 | 1,6 | 1,725 |
| 48 | 0,62 | 0,73 | 0,84 | 0,95 | 1,06 | 1,18 | 1,3 | 1,41 | 1,54 | 1,67 | 1,8 |
| 49 | 0,645 | 0,76 | 0,875 | 0,99 | 1,105 | 1,23 | 1,355 | 1,475 | 1,605 | 1,74 | 1,875 |
| 50 | 0,67 | 0,79 | 0,91 | 1,03 | 1,15 | 1,28 | 1,41 | 1,54 | 1,67 | 1,81 | 1,95 |
| 51 | 0,7 | 0,825 | 0,95 | 1,075 | 1,2 | 1,335 | 1,47 | 1,605 | 1,74 | 1,89 | 2,035 |
| 52 | 0,73 | 0,86 | 0,99 | 1,12 | 1,25 | 1,39 | 1,53 | 1,67 | 1,81 | 1,97 | 2,12 |
| 53 | 0,765 | 0,895 | 1,03 | 1,165 | 1,3 | 1,445 | 1,59 | 1,735 | 1,885 | 2,045 | 2,205 |
| 54 | 0,8 | 0,93 | 1,07 | 1,21 | 1,35 | 1,5 | 1,65 | 1,8 | 1,96 | 2,12 | 2,29 |
| 55 | 0,83 | 0,97 | 1,115 | 1,26 | 1,405 | 1,56 | 1,715 | 1,875 | 2,035 | 2,2 | 2,375 |
| 56 | 0,86 | 1,01 | 1,16 | 1,31 | 1,46 | 1,62 | 1,78 | 1,95 | 2,11 | 2,28 | 2,46 |
| 57 | 0,89 | 1,045 | 1,205 | 1,36 | 1,515 | 1,68 | 1,845 | 2,015 | 2,19 | 2,365 | 2,545 |
| 58 | 0,92 | 1,08 | 1,25 | 1,41 | 1,57 | 1,74 | 1,91 | 2,08 | 2,27 | 2,45 | 2,63 |
| 59 | 0,955 | 1,12 | 1,29 | 1,46 | 1,625 | 1,8 | 1,98 | 2,155 | 2,345 | 2,535 | 2,72 |
| 60 | 0,99 | 1,16 | 1,33 | 1,51 | 1,68 | 1,86 | 2,05 | 2,23 | 2,42 | 2,62 | 2,81 |
| 61 | 1,025 | 1,2 | 1,38 | 1,565 | 1,74 | 1,925 | 2,115 | 2,3 | 2,495 | 2,7 | 2,9 |
| 62 | 1,06 | 1,24 | 1,43 | 1,62 | 1,8 | 1,99 | 2,18 | 2,37 | 2,57 | 2,78 | 2,99 |
| 63 | 1,095 | 1,285 | 1,475 | 1,67 | 1,855 | 2,05 | 2,25 | 2,445 | 2,65 | 2,865 | 3,08 |
| 64 | 1,13 | 1,33 | 1,52 | 1,72 | 1,91 | 2,11 | 2,32 | 2,52 | 2,73 | 2,95 | 3,17 |
| 65 | 1,165 | 1,365 | 1,565 | 1,77 | 1,965 | 2,17 | 2,38 | 2,59 | 2,805 | 3,03 | 3,275 |
| 66 | 1,2 | 1,4 | 1,61 | 1,82 | 2,02 | 2,23 | 2,44 | 2,66 | 2,88 | 3,11 | 3,38 |
| 67 | 1,235 | 1,445 | 1,655 | 1,87 | 2,075 | 2,29 | 2,505 | 2,735 | 2,965 | 3,21 | 3,485 |
| 68 | 1,27 | 1,49 | 1,7 | 1,92 | 2,13 | 2,35 | 2,57 | 2,81 | 3,05 | 3,31 | 3,59 |
| 69 | 1,305 | 1,53 | 1,75 | 1,97 | 2,19 | 2,415 | 2,645 | 2,89 | 3,14 | 3,41 | 3,695 |
| 70 | 1,34 | 1,57 | 1,8 | 2,02 | 2,25 | 2,48 | 2,72 | 2,97 | 3,23 | 3,51 | 3,8 |
| 71 | 1,375 | 1,615 | 1,85 | 2,08 | 2,315 | 2,55 | 2,795 | 3,055 | 3,325 | 3,615 | 3,91 |
| 72 | 1,41 | 1,66 | 1,9 | 2,14 | 2,38 | 2,62 | 2,87 | 3,14 | 3,42 | 3,72 | 4,02 |
| 73 | 1,45 | 1,705 | 1,955 | 2,2 | 2,45 | 2,695 | 2,95 | 3,23 | 3,52 | 3,82 | 4,135 |
| 74 | 1,49 | 1,75 | 2,01 | 2,26 | 2,52 | 2,77 | 3,03 | 3,32 | 3,62 | 3,92 | 4,25 |
| 75 | 1,53 | 1,8 | 2,065 | 2,325 | 2,595 | 2,845 | 3,115 | 3,415 | 3,715 | 4,03 | 4,365 |
| 76 | 1,57 | 1,85 | 2,12 | 2,39 | 2,67 | 2,92 | 3,2 | 3,51 | 3,81 | 4,14 | 4,48 |
| 77 | 1,615 | 1,9 | 2,18 | 2,455 | 2,745 | 3 | 3,29 | 3,605 | 3,925 | 4,255 | 4,6 |
| 78 | 1,66 | 1,95 | 2,24 | 2,52 | 2,82 | 3,08 | 3,38 | 3,7 | 4,04 | 4,37 | 4,72 |
| 79 | 1,7 | 2 | 2,295 | 2,59 | 2,895 | 3,16 | 3,475 | 3,8 | 4,15 | 4,485 | 4,835 |
| 80 | 1,74 | 2,05 | 2,35 | 2,66 | 2,97 | 3,24 | 3,57 | 3,9 | 4,26 | 4,6 | 4,95 |
| 81 | 1,785 | 2,1 | 2,41 | 2,73 | 3,05 | 3,325 | 3,66 | 4,005 | 4,365 | 4,71 | 5,085 |
| 82 | 1,83 | 2,15 | 2,47 | 2,8 | 3,13 | 3,41 | 3,75 | 4,11 | 4,47 | 4,82 | 5,22 |
| 83 | 1,875 | 2,205 | 2,53 | 2,87 | 3,205 | 3,495 | 3,845 | 4,215 | 4,585 | 4,945 | 5,345 |
| 84 | 1,92 | 2,26 | 2,59 | 2,94 | 3,28 | 3,58 | 3,94 | 4,32 | 4,7 | 5,07 | 5,47 |
| 85 | 1,965 | 2,315 | 2,65 | 2,985 | 3,34 | 3,675 | 4,035 | 4,43 | 4,82 | 5,195 | 5,595 |
| 86 | 2,01 | 2,37 | 2,71 | 3,03 | 3,4 | 3,77 | 4,13 | 4,54 | 4,94 | 5,32 | 5,72 |
| 87 | 2,06 | 2,425 | 2,78 | 3,13 | 3,5 | 3,86 | 4,235 | 4,655 | 5,06 | 5,445 | 5,86 |
| 88 | 2,11 | 2,48 | 2,85 | 3,23 | 3,6 | 3,95 | 4,34 | 4,77 | 5,18 | 5,57 | 6 |
| 89 | 2,16 | 2,535 | 2,915 | 3,3 | 3,685 | 4,045 | 4,45 | 4,88 | 5,3 | 5,7 | 6,135 |
| 90 | 2,21 | 2,59 | 2,98 | 3,37 | 3,77 | 4,14 | 4,56 | 4,99 | 5,42 | 5,83 | 6,27 |
| 91 | 2,255 | 2,65 | 3,045 | 3,45 | 3,855 | 4,24 | 4,67 | 5,105 | 5,545 | 5,96 | 6,41 |
| 92 | 2,3 | 2,71 | 3,11 | 3,53 | 3,94 | 4,34 | 4,78 | 5,22 | 5,67 | 6,09 | 6,55 |
| 93 | 2,355 | 2,77 | 3,18 | 3,605 | 4,025 | 4,43 | 4,89 | 5,345 | 5,795 | 6,225 | 6,69 |
| 94 | 2,41 | 2,83 | 3,25 | 3,68 | 4,11 | 4,52 | 5 | 5,47 | 5,92 | 6,36 | 6,83 |
| 95 | 2,46 | 2,89 | 3,32 | 3,76 | 4,2 | 4,625 | 5,11 | 5,58 | 6,045 | 6,495 | 6,975 |
| 96 | 2,51 | 2,95 | 3,39 | 3,84 | 4,29 | 4,73 | 5,22 | 5,69 | 6,17 | 6,63 | 7,12 |
| 97 | 2,565 | 3,01 | 3,46 | 3,92 | 4,38 | 4,83 | 5,335 | 5,81 | 6,3 | 6,77 | 7,28 |
| 98 | 2,62 | 3,07 | 3,53 | 4 | 4,47 | 4,93 | 5,45 | 5,93 | 6,43 | 6,91 | 7,44 |
| 99 | 2,67 | 3,135 | 3,6 | 4,085 | 4,56 | 5,035 | 5,565 | 6,06 | 6,565 | 7,055 | 7,585 |
| 100 | 2,72 | 3,2 | 3,67 | 4,17 | 4,65 | 5,14 | 5,68 | 6,19 | 6,7 | 7,2 | 7,73 |
Ирина Железняк, Собкор интернет-издания «AtmWood. Дерево-промышленный вестник»
Насколько информация оказалась для Вас полезной? Loading …Похожие статьи:
| Copyright © atmwood.com.ua. Копирование материала разрешено при указании гиперссылки на источник
|
atmwood.com.ua
|
|
|
содержание .. 39 40 41 42 43 44 45 46 47 48 49 50 ..
Определение объема пиломатериалов
Определить объем пиломатериалов гораздо легче, чем круглого леса. Пиломатериалы чаще всего имеют геометрически правильную форму, поэтому объем их может быть найден путем умножения длины на толщину и ширину: V = stl, (6.11) где s – ширина пиломатериалов, см; t – толщина, мм; l – длина, м. На практике в каждом случае проделывать подобные вычисления сложно, поэтому составлены таблицы, в которых даны объемы пиломатериалов разной длины, толщины и ширины. Часть такой таблицы в качестве примера дана ниже (таблица 6.8). Преимущество таблиц объемов пиломатериалов перед таблицами объемов бревен заключается в том, что по ним можно найти с некоторыми дополнительными вычислениями объемы пиломатериалов, имеющих размеры, не указанные в таблице Таблица 6.8 – Объем досок и брусков толщиной 45 мм, шириной от 10 до 15 см и длиной до 9 м (по ОСТ )
. Например, если требуется, определить объем досок длиной 3 м, то достаточно из объема досок длиной 7 м вычесть объем досок длиной 4 м. Можно также увеличить в 3 раза объем досок длиной 1 м. Для сокращения счетных работ применяются вспомогательные таблицы, в которых показано, сколько досок разных размеров содержится в 1 м3. Для пиломатериалов устанавливается припуск на усушку по их ширине и толщине, что необходимо учитывать при приемке. Величина этого припуска колеблется от 2,5 до 7 %, причем с увеличением ширины и толщины пиломатериалов припуск уменьшается. Величина припуска в расчет кубатуры пиломатериалов не входит. Например, доски, имеющие фактическую ширину 205 мм, считаются шириной 200 мм. Разница 5 мм в данном случае и есть припуск на усушку. При определении кубатуры не обрезных досок ширину их надо измерять на середине длины. Так как ширина не обрезных досок на правой и левой сторонах может быть неодинаковой, то при обмере их надо брать среднее между шириной обеих сторон. Объем не обрезных досок определяют по их длине, ширине и толщине при помощи тех же таблиц, что и для чистообрезных пиломатериалов. У острокантных брусьев поперечное сечение квадратное или прямоугольное, поэтому площадь его находят путем решения простой геометрической задачи. Тупокантные брусья в поперечном сечении не имеют вершин углов, поэтому площадь таких поперечных сечений оказывается меньше соответствующего квадрата или прямоугольника. Для определения поперечного сечения тупокантного бруса надо его толщину а умножить на ширину b и из полученного произведения вычесть площадь недостающих четырех прямоугольных равнобедренных треугольников, у которых одна сторона l является гипотенузой. Площадь этих треугольников в сумме равна l2. Формула для определения площади поперечного сечения тупокантного бруса следующая: γ = а b – l 2, (6.12) Объем тупокантного бруса будет равен: V = (аb – l 2) L (6.13) При определении объема тупокантного бруса по этой формуле поперечное сечение берется на середине бруса. Объем острокантного бруса может быть найден по обычным объемным таблицам пиломатериалов или по формуле (6.11). Величину l2 надо выражать в процентах от поперечного сечения острокантного бруса: , (6.14) В этом случае при нахождении объемов тупокантных брусьев в зависимости от величины недостающих углов с табличных объемов надо сделать соответствующую скидку в процентах. Если у брусьев величина l (обзол) составляет более 1/5 их толщины а, то площадь сечения находят по формуле: , (6.15) где — периметр сечения бруса на его середине. При определении объемов тупокантных брусьев вместо площади срединного сечения можно брать полусумму нижнего и верхнего сечений, находимых тем же способом. Преимущество этой замены состоит в том, что измерения удобнее производить в торцах, чем на середине брусьев. Объем горбыля определяют по следующей формуле: V = g0,4L L, (6.16) где L – длина горбыля; g0,4L – площадь поперечного сечения горбыля, взятая на 0,4 длины от конца горбыля. Площадь поперечного сечения горбыля определяют по следующей формуле: , (6.17) где а – ширина горбыля; t – толщина. Обрезные и прямоугольные шпалы представляют собой тупо- и острокантные брусья, способы определения объемов которых описаны выше. Для определения объемов брусковых шпал применяют формулы срединного и среднего сечений
Рисунок 6.8 – Определение площади поперечного сечения шпалы
Для нахождения площадей поперечных сечений торцовый срез надо разделить на отдельные части и определить площадь каждой из этих частей. Наиболее целесообразно в торцовый срез шпалы вписать трапецию (рисунок 6.8), тогда определение площади поперечного сечения сведется к определению площади трапеции и двух боковых сегментов:
где а – ширина верхней постели; b – ширина нижней постели; t – толщина шпалы; l – длина непараллельной стороны трапеции, вписываемой в поперечное сечение шпалы; h – высота боковых сегментов. Все вышеприведенные вычисления обычно проводят при научных исследованиях. В практике для учёта всех перечисленных материалов применяют специальные вспомогательные таблицы.
содержание .. 39 40 41 42 43 44 45 46 47 48 49 50 ..
|
|
|
|||||
zinref.ru
