особенности оплаты, как найти формулу мощностей
Разбираясь в основных принципах электрики, важно понимать, что представляет собой активная и реактивная нагрузка. Первый тип энергии считается полезным и идет непосредственно на нужды потребителя, например, на обогрев здания, приготовление еды и работу электрических приборов. Вторая разновидность, реактивная, определяет ту часть энергии, которая не применяется для выполнения полезной работы.
Активная и реактивная мощность
Понятия активной и полной мощности могут иметь ряд противоречивых интересов со стороны клиентов и поставщиков. Потребитель пытается сэкономить на электроэнергии, оплачивая счета за расходуемые ресурсы, а поставщик ищет выгодные пути для получения полной суммы за оба типа энергии. Но есть ли способы совмещения таких требований? Да, ведь если свести объемы реактивной мощности к нулю, то это позволит приблизиться к максимальной экономии денежных средств.
Не секрет, что у некоторых потребителей электричества показатели полной и активной мощности сопоставимы. Связано это с тем, что они используют специальные приборы, нагрузка которых осуществляется с помощью резисторов.
- Лампы накаливания.
- Электрические плиты.
- Жарочные шкафы и духовки.
- Обогревательное оборудование.
- Утюги.
- Паяльники.
Для определения мощности нагрузок можно использовать знакомую со школьных времен формулу, умножив ток нагрузки на сетевое напряжение. В таком случае будут задействованы следующие единицы измерения:
- Амперы (А) — указывают на силу тока.
- Вольты (В) — характеризуют текущее напряжение.
- Ватты (Вт) — указывают на показатель мощности.
В последнее время все чаще можно замечать такую картину, что на застекленных балконах расположена тонкая блестящая пленка. Ее создают из бракованных конденсаторов, которые раньше использовались на распределительных подстанциях. Как известно, конденсаторы являются главными потребителями реактивной нагрузки, которые состоят из диэлектрика, не проводящего электрический ток (в качестве главного элемента задействуется полимерная пленка или бумага, обработанная маслом).
Для сравнения, у потребителей активной мощности роль главного элемента выполняет проводящий ток материал, такой как вольфрамовый проводник, нихромовая спираль и другие.
Емкостные нагрузки
Пытаясь понять, как найти реактивную мощность, необходимо разбираться в особенностях и принципе действия конденсаторов. Блестящие поверхности, которые расположены на балконе, являются обкладками конденсаторов из токопроводящего материала. Они отличаются способностью накапливать электроэнергию, а затем передавать ее для потребительских нужд. По сути, конденсаторы используются в качестве своеобразной аккумуляторной батареи.
А если присоединить конструкцию к источнику постоянного тока, это позволит зарядить ее кратковременным импульсом электротока, который со временем потеряет свою мощность. Для возвращения прежнего состояния конденсатора, достаточно отключить его от источника напряжения и подключить к обкладкам нагрузку. В течение какого-либо времени через нагрузку будет подаваться ток. В идеале, конденсатор должен отдать столько энергии, сколько он получил вначале.
Если подключить его к лампочке, это позволит ей на короткое время вспыхнуть, при этом неосторожный человек может даже получить незначительный удар током, если коснется к открытым контактам. Более того, если показатели напряжения довольно высокие, это может привести к фатальному исходу — смерти.
При присоединении конденсаторов к переменному току ситуация выглядит немного иначе. Так как источник переменного напряжения характеризуется свойством постоянно менять полярность, конденсаторный элемент будет постоянно разряжаться и заряжаться, пропуская переменный ток. Однако его значения не будут совпадать с напряжением источника, а составят на четверть периода больше.
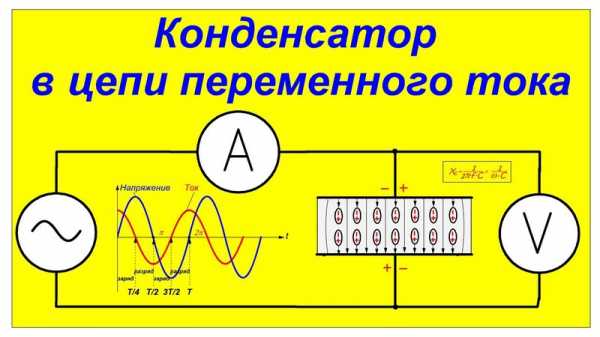
Конечные показатели будут выглядеть следующим образом: примерно половину периода конденсатор будет получать электроэнергию от источника, а другую половину — отдавать потребителю. Это значит, что суммарный показатель активной мощности составит нулевое значение. Однако из-за того, что через конденсатор постоянно протекает значительный ток, для измерения которого используется амперметр, его относят к потребителям реактивных мощностей. Формула реактивной мощности вычисляется как произведение тока на напряжение, но в этом случае единицей измерения становится вольт-ампер реактивный (ВАр), а не Вт.
Реальные потребители
Разбираясь, как найти активную мощность, люди задумываются, что будет, если попытаться подключить емкостную и индуктивную нагрузку одновременно и параллельно. В таком случае реакция будет осуществляться противоположным образом, а конечные значения начнут компенсировать себя.
При определенных обстоятельствах можно достичь идеальной компенсации, но выглядит это парадоксально: подключенные амперметры отреагируют на значительные токи, а также их полное отсутствие. Но важно понимать, что идеальных конденсаторов не существует (то же самое касается катушек индуктивности), поэтому идеализация — это условная картина для расширенного понимания процессов.
Что касается реальной ситуации, то в бытовых условиях потребители расходуют чисто активную мощность, а также смешанную активно-индуктивную. В последнем случае основными потребителями являются такие приборы:
- Электрические дрели.
- Перфораторы.
- Электрические двигатели.
- Холодильники.
- Стиральные машины.
- Другая бытовая техника.
К тому же, к таким потребителям относятся электрические трансформаторы источников питания бытового оборудования и стабилизаторов напряжения. При смешанной нагрузке, кроме полезной, потребляется еще и реактивная, при этом ее значения могут превышать показатели активной мощности. В качестве единицы измерения полной мощности используется вольт-ампер.
В электротехнике присутствует такое понятие, как «косинус фи» или коэффициент мощности. Оно указывает на отношение активной мощности к реактивной. При использовании активных нагрузок, сопоставимых с реактивными, показатель cos φ равен 1. При совмещении емкостных и индуктивных нагрузок с нулевой активной мощностью значение «косинуса фи» будет составлять нулевое значение. Если речь идет о смешанных нагрузках, то коэффициент мощности будет варьироваться от 0 до 1.
Оплата электричества
Разобравшись, как найти активную и реактивную мощность, в чем может измеряться такое значение и как описать его простым языком, остается задать логичный вопрос, за что платит реальный потребитель, пользуясь электричеством. Оплачивать полную (реактивную) энергию нет смысла. Однако в этом вопросе существует множество подводных камней, которые кроются в незначительных деталях.
Как известно, смешанная нагрузка способствует повышению тока в электросети, в результате чего могут возникать разные трудности на электростанциях, где происходит выработка электричества синхронными генераторами. Дело в том, что индуктивные нагрузки вызывают «развозбуждение» генератора, а чтобы вернуть его в начальное состояние, придется потратить реальную активную энергию, то есть переплатить массу денежных средств. Есть смысл сделать реактивную мощность платной, так как это заставит клиента компенсировать полную составляющую нагрузок.

Если возникает необходимость оплачивать оба типа мощностей по отдельности, то потребитель может рассмотреть вариант монтажа специальных батарей конденсаторов, которые будут запускаться только по графику при достижении определенного уровня потребления электроэнергии. К тому же, есть возможность выполнить монтаж профессионального оборудования в виде компенсаторов реактивной энергии, которые подключают конденсаторы при росте количества потребляемой мощности. Они эффективно поднимают «косинус фи» с 0,6 до 0,97, то есть практически до отметки 1.
К тому же, согласно текущим нормам, если клиент использовал не больше 0,15 коэффициента мощности, то он освобождается от необходимости выполнять плату за полную нагрузку. Тем не менее, большинство индивидуальных потребителей используют совсем незначительный объем электричества, поэтому проводить разделение счетов на оплату двух типов энергии нецелесообразно.
К тому же, во многих зданиях установлены однофазные счетчики, которые не способны отслеживать расход реактивных электрических нагрузок, поэтому чек за электроэнергию выставляется с учетом израсходованной активной энергии.
Полезные советы
Заниматься компенсированием индуктивных нагрузок не совсем целесообразно, так как среднестатистический потребитель использует незначительное количество активной нагрузки. Да и обустройство приборов, разделяющих потоки, требует больших вложений и выглядит сложно в техническом плане.
Подключенные конденсаторы при отключении нагрузок бесполезно нагружают электропроводку. В некоторых случаях производители счетчиков оснащают их входы компенсационными конденсаторами с индуктивной нагрузкой. При правильной конфигурации такие элементы могут снизить энергопотери, а также немного поднять напряжение на приборе путем уменьшения падения напряжения на проводе подводки.
К тому же, компенсация реактивной энергии позволит снизить уровень токов по всей линии электропитания, что положительно скажется на экономии электричества и предотвратит чрезмерные энергопотери.
220v.guru
Тема 1.14. Работа и мощность. Коэффициент полезного действия. Полезная мощность формула
Тема 1.14. Работа и мощность. Коэффициент полезного действия.
Иметь представление о мощности при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия.
Знать зависимости для определения мощности при поступательном и вращательном движениях, КПД.
Уметь рассчитать мощность с учетом потерь на трение и сил инерции.
Мощность
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени:
Единицы измерения мощности: ватты, киловатты,
Мощность при поступательном движении (рис. 16.1)
Учитывая, что S/t = vcp, получим
где F — модуль силы, действующей на тело; vср — средняя скорость движения тела.
Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Мощность при вращении (рис. 16.2)
Тело движется по дуге радиуса r из точки М1 в точку M2
Работа силы:
где Мвр — вращающий момент.
Учитывая, что
получим
где ωcp — средняя угловая скорость.
Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.
Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент.
Коэффициент полезного действия
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений. Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД):
Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:
Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.
Чем выше КПД, тем совершеннее машина.
Примеры решения задач
Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.
Решение
1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.
Полезная мощность определяется по формуле
Р = Fv cos α.
В данном случае α = 0; груз движется поступательно.
2. Скорость подъема груза
3. Необходимое усилие равно весу груза (равномерный подъем).
6. Полезная мощность Р = 3000 • 4 = 12 000 Вт.
7. Полная мощность. затрачиваемая мотором,
Пример 2. Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4.
Решение
1. Определяем полезную мощность, используемую на движение с заданной скоростью:
2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды:
Fдв = Fcопр.
3. Скорость движения судна v = 36 * 1000/3600 = 10 м/с
4. Сила сопротивления воды
Сила сопротивления воды движению судна
Fcопр. = 48 кН
Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
Решение
1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью:
Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Барабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка работала в течение t = 2 мин. Определить коэффициент полезного действия наклонной плоскости.
Решение
Как известно,
где Ап.с. — полезная работа; Адв — работа движущих сил.
В рассматриваемом примере полезная работа — работа силы тяжести
Вычислим работу движущих сил, т. е. работу вращающего момента на выходном валу лебедки:
Угол поворота барабана лебедки определяется по уравнению равномерного вращения:
где
Тогда
Подставив в выражение работы движущих сил числовые значения вращающего момента М и угла поворота φ, получим:
Коэффициент полезного действия наклонной плоскости составит
Контрольные вопросы и задания
1. Запишите формулы для расчета работы при поступательном и вращательном движениях.
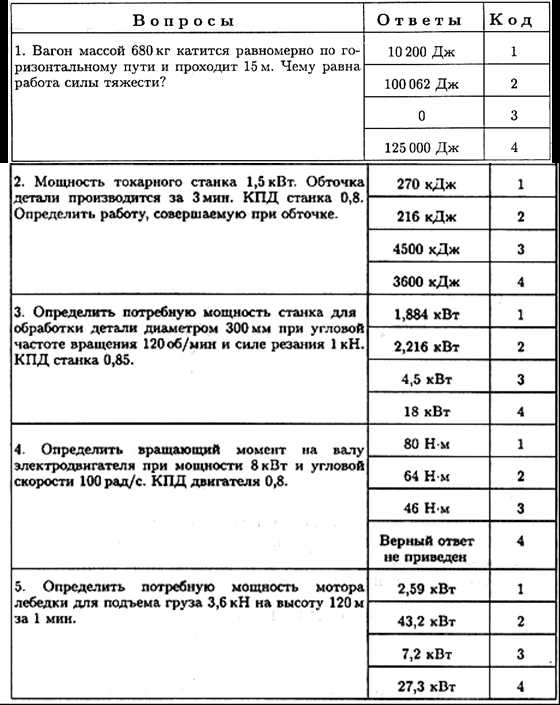
2. Вагон массой 1000 кг перемещают по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести.
3. Колодочным тормозом останавливают барабан после отключения двигателя (рис. 16.6). Определите работу торможения за 3 оборота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0,3.
4. Натяжение ветвей ременной передачи S1 = 700 Н, S2 = 300 Н (рис. 16.7). Определите вращающий момент передачи.
5. Запишите формулы для расчета мощности при поступательном и вращательном движениях.
6. Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин.
7. Определите общий КПД механизма, если при мощности двигателя 12,5 кВт и общей силе сопротивления движению 2 кН скорость движения 5 м/с.
8. Ответьте на вопросы тестового задания.
Тема 1.14. Динамика. Работа и мощность
 |
ЛЕКЦИЯ 17
infopedia.su
Мощность и коэффициент полезного действия — урок. Физика, 8 класс.
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу вре
xn—-7sbeb3bupph.xn--p1ai
это разновидность воздействия. Виды и расчеты нагрузки
Нагрузка от слова «груз» — это фактор извне, воздействующий на объект. Или количество работы, производимой объектом.
Существуют разные виды нагрузок: физическая (работа/учеба), силовая (спорт), налоговая (финансы), общественная (социум), электрическая (техника), нагрузка на транспортное средство (техническая), нагрузка на несущие конструкции (строительство) и так далее.
Физическая
В общем смысле физическая нагрузка – это выполняемая организмом двигательная активность. Обычно под этим видом нагрузки понимают трудовую деятельность, требующую физического напряжения. Это может быть работа официантом, грузчиком, разнорабочим.
Сюда же относится нагрузка умственная. То есть объем задач, которые предстоит решить. Умственная нагрузка относится к работе в целом, к учебе, решению любых жизненных проблем.
Физическая нагрузка бывает слабой, нормальной, допустимой, предельной, недопустимой.

Силовая
Это разновидность физической нагрузки, где упор делается на упражнения для прокачки мышц тела. Обычно термин силовой нагрузки используется в спорте для обозначения комплекса упражнений, цель которых – набрать мышечную массу тела.
Разделяют полную и неполную нагрузку. В первом случае тело работает во всю мощность, на грани возможного и непосильного. При неполной нагрузке мышцы работают в комфортном режиме, сохраняя тонус, но не прирастая.

Налоговая
Налоговая нагрузка – это сумма, выраженная в деньгах, которую любое предприятие (и трудоустроенное физическое лицо) обязано отчислять с бюджет государства. Из этих денег чинятся дороги, обустраиваются дворы, проводятся другие работы, а также производятся выплаты социально незащищенным слоям общества.

Общественная
Общественная нагрузка – это добровольное согласие взять на себя задачу или обязанность, связанную с общественным благоустройством, профсоюзом, партией. Эта деятельность никак не должна оплачиваться. Она проводится исключительно по инициативе добровольца.

Электрическая
Электрическая нагрузка – это фактическая суммарная электрическая мощность, потребляемая всеми приемниками, включенными в сеть. Проще говоря, это любой приемник электричества в электроцепи.

Физическая нагрузка: расчет
Из существующего разнообразия методов расчета тренировочной нагрузки можно выделить один весьма распространенный: подсчет индекса массы тела (ИМТ*) и оптимальной физической нагрузки к нему.
*ИМТ рассчитан на человека среднего телосложения с равномерным распределением жировой и мышечной массы тела.
ИМТ = масса тела, кг/(рост, м)²
Пример расчета: вес 55 кг, рост 165 см
55/(1,65)² = 55/2,7225 = 20,20
Проверяем по таблице:
| ИМТ | Значения результатов |
| <16 | Дефицит массы тела |
| 16.5—18.49 | Недостаток массы тела |
| 18.5—24.99 | Нормальная масса тела |
| 25—29.99 | Избыток массы тела |
| 30—34.99 | 1-ая степень ожирения |
| 35—39.99 | 2-ая степень ожирения |
| >40 | 3-яя степень ожирения |
Обратите внимание: данный индекс считает не жир, а общую массу тела. Можно получить результат «норма» даже при лишних жировых отложениях на некоторых участках тела. Также как и профессиональные спортсмены, легко получат «ожирение» по ИМТ, так как серьезная мышечная масса показывает избыток общего веса по приведенной таблице значений.
Нужно ли худеть, если ИМТ показывает норму, но есть лишние отложения жира в теле? Ответ — нет. Худеть не нужно, но можно вытеснять жировую ткань мышечной, то есть тренироваться. Даже при избавлении от жира весы могут не демонстрировать уменьшения веса. Это нормально и происходит как раз за счет прироста мышц.
Чтобы рассчитать какую нагрузку можно дать телу на тренировке, нужен еще один показатель — частота сердечных сокращений (ЧСС). Его можно вычислить, приложив пальцы к артерии на шее или к запястью.Нормальный показатель ЧСС в спокойном состоянии для женщин составляет 60 ударов в минуту, для мужчин — 70. У тренированных и нетренированных людей показатели нормы сердечных сокращений отличаются.
Чтобы определить оптимальную нагрузку по ЧСС, используем формулу:
| расчетный показатель | мужчина | женщина | |
| а | «пиковая» ЧСС (max) | 205 — количество лет/2 | 220 — количество лет |
| b | возможная вилка колебаний ЧСС | а — ЧСС в спокойном состоянии | а — ЧСС в спокойном состоянии |
| c | «предполагаемый сдвиг» ЧСС | (b*норма ЧСС)/100% | (b*норма ЧСС)/100% |
| d | высшая точка тренировочного диапазона | c + ЧСС в спокойном состоянии | c + ЧСС в спокойном состоянии |
Пример:
Мужчина — 35 лет, ЧСС покоя 70 уд/мин
а. 205 — 17,5 = 187,5
b. 187,5 — 70 = 117,5
c. (117,5*70)/100% = 82,25
d. 82,25 + 70 = 152,25
Женщина — 30 лет, ЧСС покоя 65 уд/мин
а. 220 — 30 = 190
b. 190 — 65 = 125
c. (125*60)/100% = 75
d. 75 + 65 = 140
Полученные результаты применяются для контроля соответствия физической нагрузки возрасту, массе и уровню физической подготовки человека.
Тренировочная зона рассчитывается как +/- 6% от высчитанной высшей точки тренировочного диапазона. В примере выше это 143 — 161,4 уд/мин для мужчины и 131,6 — 148,4 уд/мин у женщины.
После нагрузки необходимо сбавить темп, какое-то время, все еще оставаясь физически активным. Организму необходимо перестроиться на нормальный режим, для этого в конце тренировки можно перейти на легкий бег или шаг. В зависимости от интенсивности и длительности занятия это может быть как 5, так и 25 минут.
Также хорошо «заминать» тренировку растяжкой: она выравнивает дыхание и позволяет мышцам и связкам тела снова стать эластичными и не забиться после интенсивной физической активности.
fb.ru
формула, мгновенный и средний расчет силы.
Термин «мощность» в физике имеет специфический смысл. Механическая работа может выполняться с различной скоростью. А механическая мощность обозначает, как быстро совершается эта работа. Способность правильно измерить мощность имеет важное значение для использования энергетических ресурсов.

Физический смысл мощности
Разные виды мощности
Для формулы механической мощности применяется следующее выражение:
N = ΔA/Δt.
В числителе формулы затраченная работа, в знаменателе – временной промежуток ее совершения. Это отношение и называется мощностью.
Существует три величины, которыми можно выразить мощность: мгновенная, средняя и пиковая:
- Мгновенная мощность – мощностной показатель, измеренный в данный момент времени. Если рассмотреть уравнение для мощности N = ΔA/Δt , то мгновенная мощность представляет собой ту, которая берется в чрезвычайно малый промежуток времени Δt. Если имеется построенная графическая зависимость мощности от времени, то мгновенная мощность – это просто считываемое с графика значение в любой взятый момент времени. Другая запись выражения для мгновенной мощности:
N = dA/dt.
- Средняя мощность – мощностная величина, измеренная за относительно большой временной отрезок Δt;
- Пиковая мощность – максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение определенного временного промежутка. Стереосистемы и двигатели автомобилей – примеры устройств, способных обеспечить максимальную мощность, намного выше их средней номинальной мощности. Однако поддерживать эту мощностную величину можно в течение короткого времени. Хотя для эксплуатационных характеристик устройств она может быть более важной, чем средняя мощность.
Важно! Дифференциальная форма уравнения N = dA/dt универсальна. Если механическая работа выполняется равномерно в течение времени t, то средняя мощность будет равна мгновенной.
Из общего уравнения получается запись:
N = A/t,
где A будет общая работа за заданное время t. Тогда при равномерной работе вычисленный показатель равен мгновенной мощности, а при неравномерной –средней.

Формулы для механической мощности
В каких единицах измеряют мощность
Стандартной единицей для измерения мощности служит Ватт (Вт), названный в честь шотландского изобретателя и промышленника Джеймса Ватта. Согласно формуле, Вт = Дж/с.
Существует еще одна единица мощности, до сих пор широко используемая, – лошадиная сила (л. с.).
Интересно. Термин «лошадиная сила» берет свое начало в 17-м веке, когда лошадей использовали для поднятия груза из шахты. Одна л. с. равна мощности для поднятия 75 кг на 1 м за 1 с. Это эквивалентно 735,5 Вт.
Мощность силы
Уравнение для мощности соединяет выполненную работу и время. Поскольку известно, что работа выполняется силами, а силы могут перемещать объекты, можно получить другое выражение для мгновенной мощности:
- Работа, проделанная силой при перемещении:
A = F x S x cos φ.
- Если поставить А в универсальную формулу для N, определяется мощность силы:
N = (F x S x cos φ)/t = F x V x cos φ, так как V = S/t.
- Если сила параллельна скорости частицы, то формула принимает вид:
N = F x V.
Мощность вращающихся объектов
Процессы, связанные с вращением объектов, могут быть описаны аналогичными уравнениями. Эквивалентом силы для вращения является крутящий момент М, эквивалент скорости V – угловая скорость ω.
Если заменить соответствующие величины, то получается формула:
N = M x ω.
M = F x r, где r – радиус вращения.
Для расчета мощности вала, вращающегося против силы, применяется формула:
N = 2π x M x n,
где n – скорость в об/с (n = ω/2π).
Отсюда получается то же упрощенное выражение:
N = M x ω.
Таким образом, двигатель может достичь высокой мощности либо при высокой скорости, либо, обладая большим крутящим моментом. Если угловая скорость ω равна нулю, то мощность тоже равна нулю, независимо от крутящего момента.
Видео
Оцените статью:elquanta.ru
Распределенная нагрузка | Лекции и примеры решения задач механики
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м2, для объемной (например при учете собственного веса элементов конструкции) — Н/м3.
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB.
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = qmax∙AB/2,
приложенной в точке C, причем AC = 2/3AB.
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)
Рисунок 1.24
Проекция этой силы на ось Ox будет
∆Qx = q ∙ R ∙ ∆φ∙ cosφ. (1.15)
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
Qy = 0, т.е. Q = Qx, (1.16)
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м,2]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h (d – внутренний диаметр) или
F = p ∙ 2R ∙ h.
Разрывающие баллон по диаметру усилия:
S1 = S2 = S;
2S = F;
S = p∙h∙R. (1.18)
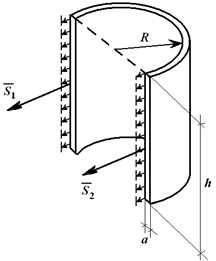
Рисунок 1.25
Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
>> Уравнения равновесия системы сил
isopromat.ru
Коэффициент мощности, формула и примеры
Определение и формула коэффициента мощности
Средняя мощность переменного электрического тока , выражаемая через действующие значения силы тока (I) и напряжение (U) равна:
где — действующее (эффективное) значение силы тока, — амплитуда силы тока, — действующее (эффективное) значение напряжения, — амплитуда напряжения.
Коэффициент мощности используют для характеристики потребителя переменного тока как реактивную составляющую нагрузки. Величина этого коэффициента отражает сдвиг фазы () переменного тока, который течет через нагрузку, по отношению к приложенному к нагрузке напряжению. Из выражения (1) видно, что по величине коэффициент мощности равен косинусу от этого сдвига. Если сила тока отстает от напряжения, то сдвиг фаз считают большим нуля, если обгоняет, то
Практическое значение коэффициента мощности
На практике коэффициент мощности стараются сделать максимально большим. Так как при малом для выделения в цепи необходимой мощности надо пропускать ток большой силы, а это приводит к большим потерям в подводящих проводах (см. закон Джоуля — Ленца).
Коэффициент мощности учитывают при проектировании электрических сетей. Если коэффициент мощности является низким, это приводит к росту части потерь электрической энергии в общей сумме потерь. Для увеличения данного коэффициента применяют компенсирующие устройства.
Ошибки при расчетах коэффициента мощности ведут к повышенному потреблению электрической энергии и уменьшению коэффициента полезного действия оборудования.
Коэффициент мощности измеряют фазометром.
Способы расчета коэффициента мощности
Коэффициент мощности рассчитывают как отношение активной мощности (P) к полной мощности (S)
где — реактивная мощность.
Коэффициент мощности для трехфазного асинхронного двигателя вычисляют при помощи формулы:
Коэффициент мощности можно определить, используя, например треугольник сопротивлений (рис.1а) или треугольник мощностей (рис.1b).
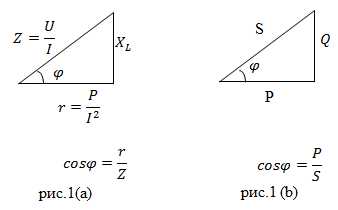
Треугольники на рис. 1(a и b) подобны, так как из стороны пропорциональны.
Единицы измерения
Коэффициент мощности — безразмерная физическая величина.
Примеры решения задач
ru.solverbook.com
Формула расчета нагрузки на фундамент. Строительство
Как известно существует несколько разных типов фундаментов. Выбор того или иного типа фундамента определяется сначала типом грунта под будущим фундаментом, а также весом будущего дома.
А величина заглубления фундамента находиться в зависимости от глубины вымерзания земли и как близко к поверхности находятся грунтовые воды.
Уметь рассчитывать фундамент нужно для того, чтоб с течением времени строение не деформировалось, не просело и не разрушилось. Более принципиально это и для рационального использования стройматериалов и экономии средств.
Правильно рассчитать фундамент может только специалист, но, используя строительные справочники, а также другие нормативные документы, можно сделать прикидочные расчеты, которые будут довольно близки к реальным.
Очень важно найти какой должна быть нагрузка на основание фундамента, чтоб грунт не просел под его давлением. Удельное сопротивление грунта – справочная величина и ее можно отыскать в нормативной документации.
Формула расчета нагрузки на фундамент:
P = P1 + Pf.
Чтоб вычислить нагрузку P, приходящуюся на основание фундамента необходимо узнать вес всего того, что находится над ним. А конкретно, вес здания P1 и вес самого фундамента Pf.
Определяем ориентировочный вес здания P1
- Он содержит в себе суммарный вес его составляющих. Всех стен здания, его перекрытий, отделки, окон и дверей, потолка и крыши, лестниц и применяемого крепежного элемента, тепло- и водоизоляционных материалов.Если используются стандартные строительные элементы (блоки фундамента, балки, тепло- и водоизоляционные покрытия, листы ДВП и т.д.), надлежащие нормативным документам, то вес определяется по их размерам и количеству.
- Следует также учитывать полезную нагрузку, создаваемую мебелью, бытовыми устройствами и наибольшим количеством людей, которые могут сразу находиться в доме. Для прикидочных расчетов ее величина обычно принимается равной произведению общей площади дома на 0,180 т/м2.
- Используя нормативные данные по региону, где планируется строительство, определяем снеговую нагрузку, которую делает слой выпавшего снега на крыше.
- Определяем силу ветра действующую на строение. Ветровая нагрузка примерно равна произведению:
S х (40 + 15h),
где S – площадь строения, а h – его высота.
Складывая все полученные величины в пунктах: 1-4 и переведя вес в тонны, получим общую примерную нагрузку, действующую на фундамент со стороны строения — P1.
Вес самого фундамента Pf
Если вес строения для всех типов фундаментов считается одинаково, то вес самого фундамента будет подсчитываться по-разному.
1. Расчет нагрузки на ленточный фундамент
Вес фундамента (Pf) в данном случае рассчитывается по формуле:
Pf = V x q,
где q – плотность материала, из которого изготовлен фундамент (определяется по нормативам СНиП), а V – его объем, равный произведению площади опоры фундамента (S) на его высоту (H):
V = S x H;
Зная общую нагрузку на основание ленточного фундамента P и его площадь опоры S, определим величину P/S. Чтоб учесть погрешности в выборе начальных данных, ее значение должно быть на 15-20% меньше R, расчетного сопротивления грунта, определяемого по справочнику.
2. Расчет столбчатого фундамента
Общая нагрузка, действующая на грунт от подошвы столбчатого фундамента, складывается из распределенного веса строения плюс веса самого столба. Опорная площадь столба – Ss, высота – H.
Тогда его объем равен: V = Ss x H, а вес Ps = V x q, где q– плотность материала, из которого сделан столб. Если полное количество столбов N, то общий вес фундамента равен:
Pf = Ps х N,
а общая площадь опоры:
S = Ss x N.
3. Расчет свайного фундамента из заостренных либо готовых винтообразных свай.
Заостренные концы таких свай уменьшают нагрузку на грунт и не дают выталкивать их при замерзании земли. Нужное количество свай зависит от общего веса будущего здания.
Если известно количество винтообразных опор — N и вес сооружения P, то несущая способность одной опоры равна P / N. Выбираем более подходящие готовые сваи с известной несущей способностью и длиной, беря во внимание геологические особенности местности и грунта.
Задачам расчета фундаментов посвящено много веб-сайтов.
На сайте http://stroy-svoimi-rukami.ru/fundament/view/22/ можно не только отыскать подробные объяснения, но также найти полезные таблицы.
Теоретические базы устройства фундаментов изложены тут — http://teoriastroiki.ru/spravochnik/fundament/grunty_i_osnovaniya/raschet_fundamenta/
С примерами расчета определенных фундаментов можно также ознакомиться на веб-сайтах:
http://ibud.ua/ru/statya/raschet-fundamenta-primer-rascheta-fundamenta-2992
http://stroy-shkola.ru/fundament/raschet-nagruzki-na-fundament.html
Бесплатными онлайн калькуляторами для строй расчетов можно пользоваться тут:
http://www.zhitov.ru/
http://st-mater.narod.ru/index2.html
http://m350.ru/calculator/
teletap.org