Энергия и мощность электрического тока
В любой замкнутой электрической цепи источник затрачивает электрическую энергию Wистна перемещение единицы положительного заряда по всей цепи: и на внутреннем и на внешнем участках.
и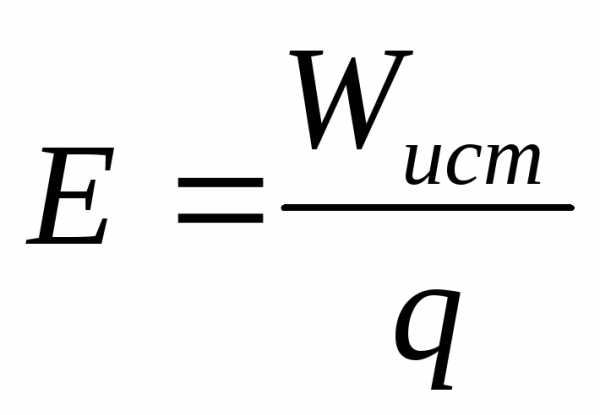 ;
;
Энергия источника определяется выражением: Wист=Eq=EIt= (U0+U)It;
Энергия источника (полезная), которая расходуется на потребителе: W=UIt;
Энергия источника (потери), которая расходуется на внутреннем сопротивлении источника: W=U0It;
Преобразование электрической энергии в другие виды энергий происходит с определенной скоростью. Эта скорость определяет электрическую мощность элементов электрической цепи:
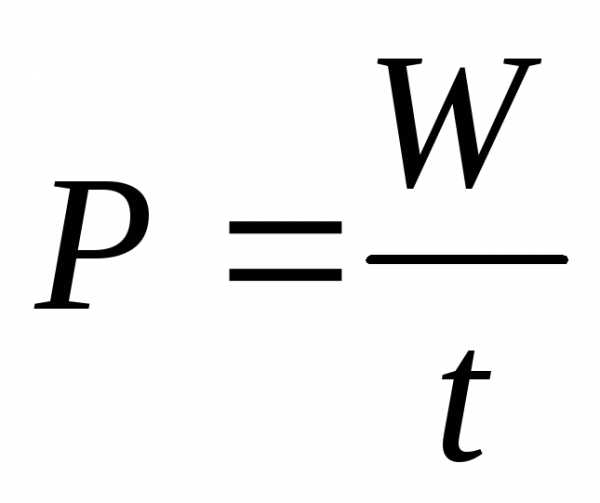 ;
;
Мощность источника определяется соотношением:
Мощность потребителя определяется соотношением:
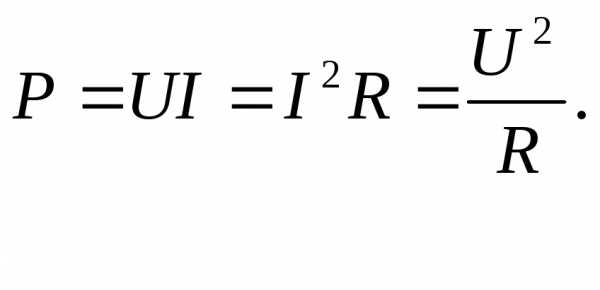
Коэффициент полезного действияэлектрической цепиηопределяется отношением мощности потребителя к мощности источника:
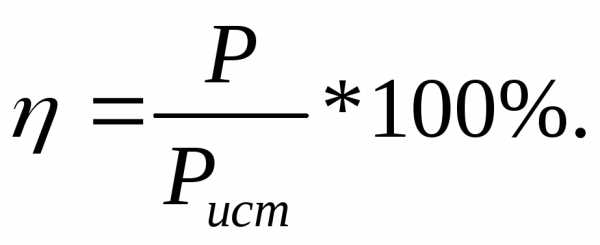
Закон Джоуля — Ленца
Ток, протекая по проводнику, нагревает его (в этом случае электрическая энергия преобразуется в тепловую). Количество выделенного тепла будет определяться количеством электрической энергии, затраченной в этом проводнике.
Дж.
(кал).
Коэффициент 0,24 (электротермический эквивалент) устанавливает зависимость между электрической и тепловой энергией.
Часть3: Режимы работы электрических цепей
В электрических цепях все основные элементы делятся на активные и пассивные. Активными считаются элементы, в которых преобразование энергии сопровождается возникновением ЭДС (аккумуляторы, генераторы). Элементы, в которых ЭДС не возникает, называются пассивными.
Параметры электрических цепей:
Ток в замкнутой цепи 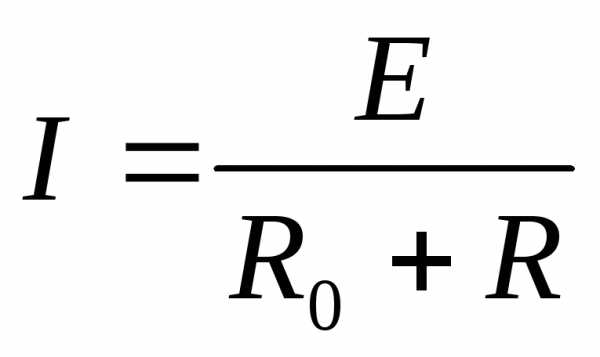 ;
;
Напряжение на клеммах источника ;
Падение напряжения на сопротивлении
источника 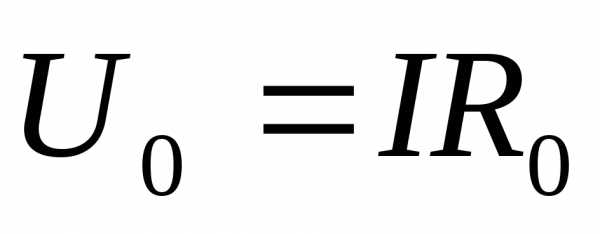 ;
;
Полезная мощность (мощность потребителя) .
Электрические цепи могут работать в трех режимах:
Условие максимальной отдачи мощности: полезная мощность максимальна, когда сопротивление потребителя
КПД при максимальной отдаче мощности равно 50%, к 100% КПД приближается в режиме, близком к холостому ходу.
Нормальным (рабочим) режимом называют такой режим работы цепи, при котором ток, напряжение и мощность не превышают номинальных значений, заданных заводом-изготовителем.
Источники тока могут работать в режиме генератора и в режиме нагрузки. Источники, ЭДС которых совпадают с направлением тока в цепи, работают в режиме генератора, а источники , ЭДС которых не совпадают с направлением тока, работают в режиме потребителя.
Напряжение источника, работающего в режиме генератора: .
Напряжение источника, работающего в режиме потребителя: .
Тема 1.3
Расчет электрических цепей постоянного тока
Основной целью расчета электрической цепи является нахождение ее параметров: ток, напряжение, сопротивление, мощность, КПД. Значения параметров дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Для расчета электрических цепей основой служат законы Ома и Кирхгофа, Джоуля-Ленца.
Законы Кирхгофа
К характерным элементам электрической цепи относятся ветвь, узел, контур.
Ветвью электрической цепи называется ее участок, на всем протяжении которого величина тока имеет одинаковое значение. Ветви, которые содержат источники питания называются активными, а которые не содержат их – пассивными.
Узлом электрической цепи называется точка соединения электрических ветвей.
Контуром электрической цепи называют замкнутое соединение, в которое могут входить несколько ветвей.
Первый закон Кирхгофа
Сумма токов входящих в узел равна сумме токов, выходящих из узла. ИЛИ Сумма токов, сходящихся в узле равна нулю.
∑I=0; — математическое выражение первого закона Кирхгофа.
Второй закон Кирхгофа
Алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи.
; — математическое выражение второго закона Кирхгофа.
Последовательное соединение потребителей
Последовательным соединением участков эй цепи называют соединение, при котором через все участки цепи проходит один и тот же ток.
Общее напряжение последовательно соединенных элементов равно сумме напряжений на каждом элементе согласно второму закону Кирхгофа: ;
В соответствии с законом Ома: ; Из этого соотношения следует:; Таким образом, общее сопротивление цепи с последовательно соединенными элементами равно сумме этих сопротивлений.
Параллельное сопротивление потребителей
Параллельным соединением участков электрической цепи называется соединение, при котором все участки цепи присоединяются к одной паре узлов, то есть находятся под действием одного и того же напряжения.
Общий ток такого соединения согласно первому закона Кирхгофа будет равен сумме токов в отдельных ветвях: ; В соответствии с законом Ома:; Если поделить левую и правую части на
Обратная величина общего эквивалентного сопротивления параллельно включенных потребителей равна сумме обратных величин этих потребителей.
Величина, обратная сопротивлению определяет проводимость потребителя g. Тогда для параллельно соединенных потребителей справедливо:;
studfiles.net
Формулы для расчета электрических величин.
Проводя диагностику и ремонт холодильников Стинол, мастер периодически сталкивается с необходимостью проводить измерения электрических величин. По результатам измерения делаются выводы о работоспособности той или иной детали электрооборудования холодильника.Обозначения:
I — Сила тока в цепи, единицы измерения — Амперы (А)
U — Напряжение, единицы измерения — Вольты (В)
R — Сопротивление нагрузки, единицы измерения — Омы (Ом)
Эти электрические величины связаны друг с другом следующими формулами:
I=U/R
P=IU
Электрооборудование холодильников Стинол рассчитано на питание от сети переменного тока напряжением 220 Вольт. Соответственно, вместо «U» в формулы можем смело подставлять число 220. Путем нехитрых перестановок получаем следующую кучу формул на любой случай:
I=220/R
I=P/220
R=220/I
R=48400/P
P=220·I
P=48400/R
Важно! В цепях переменного тока данные формулы справедливы только для активной нагрузки, сопротивление которой переменному току не зависит от его частоты. Для реактивных потребителей (емкости и индуктивности) эти равенства выполняться уже не будут. А это значит, что по большому счету, при ремонтах холодильников Стинол всю эту математику мы можем применять только к нагревателям системы No Frost. А различные электродвигатели (мотор-компрессор, вентилятор, микродвигатель таймера и т.п.), являясь нагрузкой реактивной (индуктивной) автоматически из подобных рассчетов выпадают.
Во время работы удобно иметь под рукой табличку для быстрого взаимного пересчета электрической мощности, сопротивления и силы тока. Подобная табличка представлена ниже, в свое время она была составлена мной для быстрого ориентирования в параметрах нагревателей оттайки различных импортных холодильников. Специалисту по ремонту холодильников Стинол она тоже может оказаться полезной.
Пользоваться таблицей достаточно просто:
• Измерив мультиметром сопротивление нагревателя, и найдя соответствующую строчку в таблице, сразу становится ясно, какой мощностью он обладает и какой ток потечет через него при подаче питающего напряжения 220 Вольт.
• Узнав при помощи токовых клещей, какой ток потребляет нагреватель, по таблице можно выяснить его сопротивление и мощность.
• Узнав по маркировке нагревателя его мощность, легко выяснить его сопротивление и ток.
| сила тока, А | мощность, W | сопротивление, Ом |
| 0.01 | 2.2 | 22k |
| 0.05 | 11 | 4.4k |
| 0.1 | 22 | 2.2k |
| 0.2 | 44 | 1.1k |
| 0.3 | 66 | 733 |
| 0.4 | 88 | 550 |
| 0.5 | 110 | 440 |
| 0.6 | 132 | 366 |
| 0.7 | 154 | 314 |
| 0.8 | 176 | 275 |
| 0.9 | 198 | 244 |
| 1 | 220 | 220 |
| 1.1 | 242 | 200 |
| 1.2 | 264 | 183 |
| 1.3 | 286 | 169 |
| 1.4 | 308 | 157 |
| 1.5 | 330 | 146 |
| 1.6 | 352 | 138 |
| 1.7 | 374 | 129 |
| 1.8 | 396 | 122 |
| 1.9 | 418 | 116 |
| 2 | 440 | 110 |
| 2.1 | 462 | 105 |
| 2.2 | 484 | 100 |
| 2.3 | 506 | 96 |
| 2.4 | 528 | 92 |
| 2.5 | 550 | 88 |
| 2.6 | 572 | 85 |
| 2.7 | 594 | 81 |
| 2.8 | 616 | 79 |
| 2.9 | 638 | 76 |
| 3 | 660 | 73 |
| 3.1 | 682 | 71 |
| 3.2 | 704 | 69 |
Распечатать таблицу удобно с этой страницы
www.stinol-repair.ru
Мощность тока в электрических цепях :: SYL.ru
Одним из параметров, характеризующих поведение электронов в электрической цепи, кроме напряжения и тока, выступает мощность. Она является мерой количества работы, которую можно совершить за единицу времени. Работу обычно сравнивают с подъёмом веса. Чем больше вес и высота его подъёма, тем больше работы выполнено. Мощность определяет быстроту совершения единицы работы.
Единицы измерения
Мощность автомобилей исчисляют в лошадиных силах – единице измерения, придуманной изготовителями паровых двигателей с целью измерения работоспособности своих агрегатов в обычном источнике энергии того времени. Мощность автомобиля не говорит, как высоко он может заехать на холм или сколько веса он может перевезти, а только показывает, как быстро он это сделает.
Мощность двигателя зависит от его скорости и вращающего момента выходного вала. Скорость измеряют в оборотах в минуту. Вращающий момент – это момент силы двигателя, который измерялся первоначально в фунт-футах, а сейчас в ньютон-метрах или джоулях.
Тракторный двигатель в 100 л. с. вращается медленно, но с большим крутящим моментом. Мотоциклетный двигатель равной мощности вращается быстро, но с небольшим крутящим моментом. Уравнение расчёта мощности имеет вид:
P = 2π S T / 33000, где S – скорость вращения, об/мин, а T – момент вращения.
Переменными здесь являются момент и скорость. Иначе говоря, мощность прямо пропорциональна ST: P~ST.
Мощность постоянного тока
В электроцепях мощность находится в функциональной зависимости от напряжения и тока. Неудивительно, что она похожа на вышеприведённое уравнение P=IU.
Но тут P не пропорциональна току, умноженному на напряжение, а равняется ему. Исчисляется в ваттах, сокращённо Вт.
Важно знать, что ток и напряжение отдельно мощность не определяют, лишь их совокупность. Напряжение является работой на единицу электрического заряда, а ток – скоростью движения зарядов. Напряжение (эквивалент работы) подобно работе при подъёме веса в противодействие силе гравитации. Ток (эквивалентен скорости) подобен скорости подъёма веса. Их произведение и составляет мощность.
Как тракторный и мотоциклетный моторы, цепь с высоким напряжением и небольшим током способна быть одинаковой мощности с цепью невысокого напряжения и большим током. Напряжение и ток вне взаимосвязи не могут характеризовать мощность электроцепи.
Разомкнутая цепь с напряжением и нулевой силой тока работы не совершает, вне зависимости от высоты напряжения. Ведь, согласно формуле, что угодно, умноженное на 0, даёт 0: P = 0 U = 0. В замкнутой цепи из сверхпроводящего провода с нулевым сопротивлением можно достичь тока при напряжении, равном нулю, что также не приведёт к рассеиванию энергии: P = I 0 = 0.
Лошадиные силы и ватты обозначают одно и то же: количество работы, которую можно совершить за единицу времени. Эти единицы взаимосвязаны соотношением
1 л. с. = 745,7 Вт

Пример расчёта
Итак, мощность тока электроцепи в ваттах равняется произведению напряжения на ток.
Чтобы определить, например, мощность нагрузки сопротивлением 3 Ом, в цепи с батареей питания напряжением 12 В, необходимо, применив закон Ома, найти ток
I = U/R = 12/3 =4 А
Умножение полученной силы тока на напряжение и даст искомый результат:
P = I U = 4 А 12 В = 48 Вт
Таким образом, лампа потребляет 48 Вт.
Что же произойдёт при увеличении напряжения?
При напряжении 24 В и сопротивлении 3 Ом ток
I= U/R = 24/3 =8 А
При удвоении напряжения удвоилась и сила тока.
P = IU = 8 А 24 В = 192 Вт
Мощность также увеличилась, но больше. Почему? Потому что это функция произведения напряжения на ток, напряжение и ток увеличились в 2 раза, следовательно, мощность возросла в 4 раза. Это можно проверить делением 192 ватт на 48, частное от которого равно 4.
Варианты формулы
Применив алгебру для преобразования формулы, можно взять исходное уравнение и преобразовать его для случаев, когда неизвестен один из параметров.
Если даны напряжение и сопротивление:
P = (U/R) U или P = U2/R
При известной силе тока и сопротивлении:
P = I (I R) или P = I2 R
Исторический факт: отношение между рассеиваемой мощностью и силой тока через сопротивление открыл Джеймс Прескотт Джоуль, а не Георг Симон Ом. Оно было опубликовано в 1841 г. в виде уравнения P = I2 R и носит название закона Джоуля–Ленца.
Уравнения мощности:
Переменный ток
Закон Ома и Джоуля–Ленца были установлены для постоянного тока, но они справедливы и для мгновенных значений изменяющегося тока и напряжения.
Мгновенное значение P равно произведению мгновенных значений силы тока и напряжения с учётом их смещения по фазе на угол φ:
P(t) = U(t)I(t) = Um cosωt Im cos(ωt-φ) = (1/2)Um Im cosφ + (1/2) Um Im cos(2ωt-φ).
Из уравнения следует, что у мгновенной мощности есть постоянная составляющая, и она совершает колебательные движения вокруг среднего значения с частотой, которая вдвое превышает частоту тока.
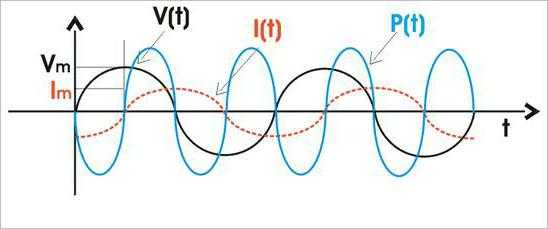
Среднее значение P(t), представляющее практический интерес, равно:
P = (UmIm/2) cosφ
С учётом того, что cos φ=R/Z, где Z=(R2 + (ωL — 1/ω C)2)1/2 и Um/Z = Im,
P = (R Im2)/2
Здесь I = Im 2-1/2 = 0,707 Im – эффективное значение силы тока, А.
Аналогично U = Um2-1/2 = 0,707 Um – эффективное напряжение, В.
Средняя мощность через эффективное напряжение и ток определяется
P = U I cos φ, где cos φ – коэффициент мощности.
P в электроцепи переходит в тепловую или другой вид энергии. Наибольшей активной мощности можно достичь при cosφ=1, то есть при отсутствии сдвига фаз. Она носит название полной мощности
S = U I = Z I2 = U2/Z
Её размерность совпадает с размерностью P, но с целью отличия S измеряется вольт-амперами, ВА.
Степень интенсивности обмена энергией в электроцепи характеризуется реактивной мощностью
Q = U I sinφ = U Ip = Up I = X I2 = U2/X
Она имеет размерность активной и полной, но с целью различения её выражают вольт-амперами реактивными, ВАр.
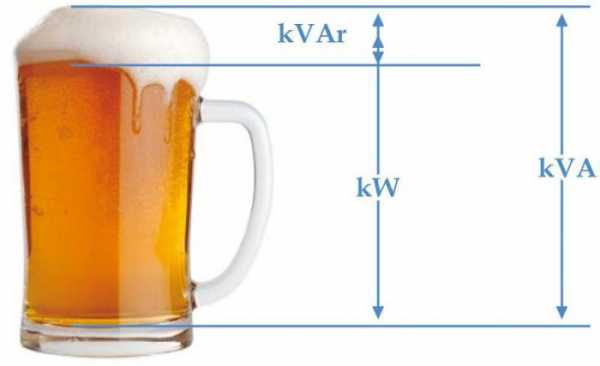
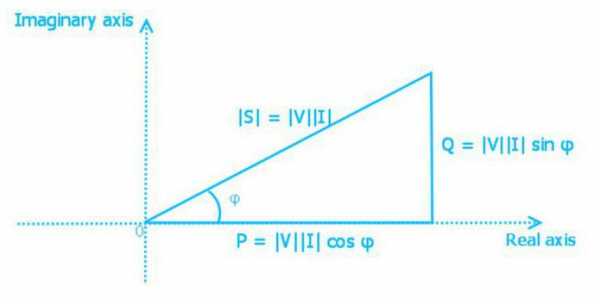
Треугольник мощностей
Мощность активная, реактивная и полная взаимосвязаны выражением
S = (P 2+ Q2)1/2
Мощность представляют в виде стороны прямоугольного треугольника. Используя законы тригонометрии, можно найти длину одной стороны (количество мощности любого типа) по двум известным сторонам или по длине одной и углу. В таком треугольнике активная мощность является прилежащим катетом, реактивная – противолежащим, а полная мощность – гипотенузой. Угол между катетом активной мощности и гипотенузой равен углу фазы импеданса Z электрической цепи.
Комплексная форма записи этой взаимосвязи следующая:
S = P+jQ = U I cosφ + j U I sinφ= U I ejφ = U I*, где
S – комплексная мощность;
I* – комплексное сопряжённое значение тока.
Вещественная составляющая комплекса – активная, а мнимая – реактивная.
Мгновенная полная мощность всегда остаётся постоянной величиной.
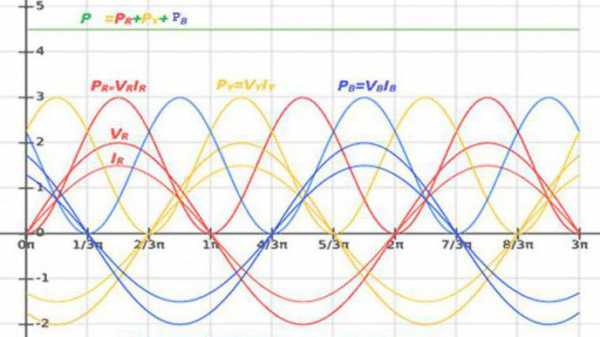
Мощность трёхфазного тока
Нагрузка каждой фазы трёхфазной электроцепи преобразует энергию или обменивается ею с источником питания. Вследствие этого P и Q цепи равняются суммарной мощности всех фаз:
P = Pr+ Py+ Pb; Q = Qr+ Qy+ Qb – соединение «звезда»;
P = Pry+ Pyb+ Pbr; Q = Qry+ Qyb+ Qbr – соединение «треугольник».
Активные и реактивные мощности каждой фазы определяются, как в однофазной цепи.
Полная мощность трёхфазной цепи:
S = (P2+Q2)1/2,
что в комплексной форме имеет вид
S = P+jQ = (Pr + Py + Pb) + j(Qr + Qy + Qb )= Sr + Sy + Sb= Ur Ir + Uy Iy + Ub Ib
Симметричная нагрузка фаз имеет следствием равенство их мощностей. Вот почему мощность тока равна утроенной активной и реактивной мощности фазы:
P = 3Pф = 3 Iф Uфcosφф = 3 Rф Iф2
Q = 3 Qф = 3 Iф Uф sinφф = 3 Xф Iф2
S = 3 Sф = 3 Iф Uф
Iф и Uф здесь можно заменить их линейными значениями, учитывая, что для звезды Uф=Uл; Iф=Iл, а для треугольника Uф=Uл; Iф=Iл3-1/2:
P = 31/2 Iл Uлcosφф;
Q = 31/2 Iл Uлsinφф;
S = 31/2 Iл Uл.
Ток несинусоидальной формы
Определение P в цепи несинусоидального тока аналогично её определению в цепи тока синусоидального, так как за период T средняя мгновенная мощность
P = 1/T∫u i dt
Активная мощность тока определяется суммой P гармонических составляющих, в том числе и постоянной, являющейся гармоникой нулевой частоты.
Реактивная мощность тока подобным образом является результатом сложения Q каждой гармоники.
Q = ∑Uk Ik sinφk = ∑ Qk
Полная мощность определяется произведением эффективного тока и напряжения:
S = I U.
www.syl.ru
Мощность в цепи постоянного тока, электрическая энергия и коэффициент полезного действия
Электрическая мощность Р (Вт) определяется произведением напряжения на силу тока:
P = U•I
где U — напряжение на токоприемнике, В; I — сила тока через токоприемник, А.
Единица мощности — 1 ватт = 1 вольт х 1 ампер.Принимая во внимание закон Ома (U = IR; I = U/R), равенство (2.28) можно представить следующим образом:
P = 12R. (2.29)
Р = U2/R. (2.30)
В практике пользуются производной единицей мощности — киловатт (кВт), 1 кВт = 1000 Вт. Как и в механике электрическая энергия, или р а б о т а(Дж), равна произведению мощности на время:
W= Pt, (2.31)
где Р — мощность, Вт; t — время, с. Единица энергии 1 джоуль = 1 ватт х 1 секунду. В практике пользуются значительно более крупной единицей — киловатт-часом (кВт • ч),1 кВт-ч = 1 кВт-1 ч = 1000 Вт-3600 с = 3 600 000 Дж = 3,6 МДж. Если взять значение Р из выражений (2.28), (2.29) и (2.30), то формулу (2.31) можно переписать так:
. U2
W= U It = —— •t = I2R•t. (2.32)
. R
Пример 1. Нагревательный прибор, включенный в сеть 220 В, потребляет ток 5 А.Сколько энергии расходуется за сутки? Решение. Количество энергии W = 220 ■ 5 • 24 = 26 400 Вт • ч = 26,4 кВт • ч = 95,04 МДж.
Пример 2. Какова мощность нагревательного прибора, если за 5 ч потребляемая имэнергия составила 10 кВт ч?
Решение. Мощность прибора Р = w/t = 10/5 = 2 кВт. Тепловое действие тока. Прохождение электрическоготока через проводник сопровождается выделением тепла. В нагревательных приборах получение тепла — это конечная цель. Но в другихприборах и устройствах выделение тепла представляет собой непроизводительные потери электрической энергии. Количество теплоты измеряют в джоулях, причем 1 Дж = 1 Вт-1 с = 1 Вт·с.
По закону Ленца—Джоуля количество теплоты Q, выделяемой то-ком в проводнике, пропорционально квадрату тока, сопротивлению проводника и времени прохождения тока:
Q =I2RTT (2.33)
где I — сила тока, A; R — сопротивление, Ом; t — время, с.
Пример 3. Найти количество теплоты, которое выделяется на сопротивлении R = 20 Ом в течение t = 1 ч при протекании тока / = 10 А. Решение. Искомое количество теплоты
Q = 100 ■ 20 ■ 3600 = 7200 кДж;
При всяком превращении одного вида энергии в другой наблюдаются потери энергии. Например, при превращении электрической энергии в механическую (в электрическом двигателе) часть электроэнергии, потребляемой электродвигателем из сети, расходуется на нагрев двигателя, на трение в подшипниках и т. д.
Этот процесс количественно характеризует величина, называемая коэффициентом полезного действия (к.п.д.). Под к.п.д понимают отношение полезной мощности Рпол, отдаваемой машиной, к подведенной мощности Pподв:
ή = Pпол/Pподв. . (2.34)
Пример 4. Водонагревательный прибор потребляет из сети мощность, равную 1 кВт, причем 50 л воды нагреваются на 80°С в течение 5 ч. Каков к.п.д. водонагревателя?
Решение. Потребляемая из сети за 5 ч электроэнергия W=Pt = 1•5=5 кВтч = 5000-3600 Дж.
Для нагревания 50 л воды на 80°С используется энергия, равная
Wпол=cV(t2—t1) =4,19-50 000-80 Дж,
где с =4,19 — теплоемкость воды, Дж/см3оС.
Часть энергии, равная разности Wподв— Wпол, теряется при охлаждении нагревателя.
. Wпол 4,19•-50 000• 80 4,19
Тогда к.п.д. ή = ——— = —————————— = ——— = 0,93, или 93%
. Wподв 5000•3600 4,5
где Wпол—энергия, израсходованная на нагрев воды; Wподв—энергия, выделившаяся в нагревателях.
www.rural-electrician.ru
Мощность в цепи переменного тока
Мощность в цепи переменного тока.
В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теориикомплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ(сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность
Единица измерения — ватт (W, Вт).
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ —угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
studfiles.net
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: | Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). | Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… | 2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). | 4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: — чем больше сопротивление, тем больше напряжение. | 4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: — чем больше сопротивление, тем меньше сила тока. |
www.eduspb.com
Электрическая мощность — это… Что такое Электрическая мощность?
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:
Для единичного заряда на участке A-B:
Для всех зарядов:
Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:
Если участок цепи содержит резистор c электрическим сопротивлением R, то
Дифференциальные выражения для электрической мощности
Мощность, выделяемая в единице объёма, равна:
В линейном изотропном приближении:
В линейном анизотропном приближении (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла):
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
| где — ЭДС. |
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.
Мощность переменного тока
В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность
Единица измерения — ватт (W, Вт).
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность
Единица измерения — вольт-ампер реактивный (var, вар)
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.[источник не указан 124 дня]
Полная мощность
Единица полной электрической мощности — вольт-ампер (V·A, В·А)
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность
Мощность, аналогично импедансу, можно записать в комплексном виде:
- где — комплексное напряжение, — комплексный ток, — импеданс, * — оператор комплексного сопряжения.
Модуль комплексной мощности равен полной мощности S. Действительная часть равна активной мощности Р, а мнимая — реактивной мощности Q с корректным знаком в зависимости от характера нагрузки.
Неактивная мощность
Неактивная мощность (пассивная мощность)[источник не указан 172 дня] — это мощность нелинейных искажений тока, равная корню квадратному из разности квадратов полной и активной мощностей в цепи переменного тока. В цепи с синусоидальным напряжением неактивная мощность равна корню квадратному из суммы квадратов реактивной мощности и мощностей высших гармоник тока[источник не указан 172 дня]. При отсутствии высших гармоник неактивная мощность равна модулю реактивной мощности.
Под мощностью гармоники тока понимается произведение действующего значения силы тока данной гармоники на действующее значение напряжения[источник не указан 172 дня].
Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы[источник не указан 172 дня]. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной.
Связь неактивной, активной и полной мощностей
Величину неактивной мощности обозначим N. Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения:
Представим вектор тока i в виде суммы двух ортогональных составляющих ia и ip, которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть ia = λu, где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем
Запишем выражение для активной мощности P, скалярно умножив последнее равенство на u:
Отсюда находим
Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность.
Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность:
Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе.
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон — ГЭТ 153-86 Государственный специальный эталон единицы электрической мощности в диапазоне частот 40-2500 Гц. Институт-хранитель: ВНИИМ
Мощность некоторых электрических приборов
В таблице указаны значения мощности некоторых потребителей электрического тока:
| Электрический прибор | Мощность,Вт |
|---|---|
| Лампочка фонарика | 1 |
| Лампа люминесцентная бытовая | 5…30 |
| Лампа накаливания бытовая | 25…150 |
| Холодильник бытовой | 15…200 |
| Электропылесос | 100…2 000 |
| Электрический утюг | 300…2 000 |
| Стиральная машина | 350…2 000 |
| Электрическая плитка | 1 000…2 000 |
| Сварочный аппарат бытовой | 1 000…5 500 |
| Двигатель трамвая | 45 000…50 000 |
| Двигатель электровоза | 650 000 |
| Электродвигатели прокатного стана | 6 000 000…9 000 000 |
Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная.
Литература
- ГОСТ 8.417-2002 Единицы величин
- ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации
- Бессонов Л. А. Теоретические основы электротехники. — М: Высшая школа, 1984.
- Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193—2009. — 146 с.
Дополнительная литература
- Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
- Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
- Агунов М. В., Агунов А. В., Вербова Н. М. Определение составляющих полной мощности в электрических цепях с несинусоидальными напряжениями и токами методами цифровой обработки сигналов // Электротехника, 2005, № 7, С. 45-48.
- Агунов А. В. Неактивные составляющие полной мощности в автономных электротехнических системах судостроения. Автореферат диссертации на соискание ученой степени кандидата технических наук. СПб., СПбГМТУ, 1997, 20 с.
- Агунов М. В. Энергетические процессы в электрических цепях с несинусоидальными режимами и их эффективность. Кишинев-Тольятти: МолдНИИТЭИ, 1997, 84 с.
- Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
- Агунов А. В. Управление качеством электроэнергии при несинусоидальных режимах. СПб., СПбГМТУ, 2009, 134 с.
- Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
- Агунов А. В. Статический компенсатор неактивных составляющих мощности с полной компенсацией гармонических составляющих тока нагрузки // Электротехника, 2003, № 2, С. 47-50.
Ссылки
См. также
biograf.academic.ru