Как найти мощность тока — формулы с примерами расчетов

В физике достаточно много внимания уделено энергии и мощности устройств, веществ или тел. В электротехнике эти понятия играют не менее важную роль чем в других разделах физики, ведь от них зависит насколько быстро установка выполнит свою работу и какую нагрузку понесут линии электропередач. Исходя из этих сведений подбираются трансформаторы для подстанций, генераторы для электростанций и сечение проводников передающих линий. В этой статье мы расскажем, как найти мощность электрического прибора или установки, зная силу тока, напряжение и сопротивление.

• Определение
• Формулы для расчётов цепи постоянного тока
• Для переменного тока
• Пример расчёта полной мощности для электродвигателя
• Расчет для параллельного и последовательного подключения
• Заключение

Определение

Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:

P=dA/dt

Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.

Электрическая мощность равна произведению тока на напряжение или:

P=UI

Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.

Формулы для расчётов цепи постоянного тока

Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:

P=UI

Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:

P=U²/R

Также можно выполнить расчет, зная ток и сопротивление:

P=I²*R

Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.

Для переменного тока

Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.

Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:

S=UI

Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.

P=UIcosФ

Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.

Q=UIsinФ

Или выразить из этого выражения:

И отсюда вычислить искомую величину.

Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:

S=3U_фI_ф

А зная Uлинейное:

S=1,73*U_лI_л

1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.

Тогда по аналогии чтобы найти P активную:

P=3U_фI_ф*cosФ=1,73*U_лI_л*cosФ

Определить реактивную мощность можно:

Q=3U_фI_ф*sinФ=1,73*U_лI_л*sinФ

На этом теоретические сведения заканчиваются и мы перейдём к практике.

Пример расчёта полной мощности для электродвигателя

Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.

Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:

1. P_{на валу}=160 кВт = 160000 Вт
2. n=0,94
3. cosФ=0,9
4. U=380

Тогда найти активную электрическую мощность можно по формуле:

P=P_{на валу}/n=160000/0,94=170213 Вт

Теперь можно найти S:

S=P/cosφ=170213/0,9=189126 Вт

Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.

Расчет для параллельного и последовательного подключения

При расчете схемы электронного устройства часто нужно найти мощность, которая выделяется на отдельном элементе. Тогда нужно определить, какое напряжение падает на нём, если речь идёт о последовательном подключении, или какая сила тока протекает при параллельном включении, рассмотрим конкретные случаи.

Здесь Iобщий равен:

I=U/(R1+R2)=12/(10+10)=12/20=0,6

Общая мощность:

P=UI=12*0,6=7,2 Ватт

На каждом резисторе R1 и R2, так как их сопротивление одинаково, напряжение падает по:

U=IR=0,6*10=6 Вольт

И выделяется по:

P_{на резисторе}=UI=6*0,6=3,6 Ватта

Тогда при параллельном подключении в такой схеме:

Сначала ищем I в каждой ветви:

I₁=U/R₁=12/1=12 Ампер

I₂=U/R₂=12/2=6 Ампер

И выделяется на каждом по:

P_R1=12*6=72 Ватта

P_R2=12*12=144 Ватта

Выделяется всего:

P=UI=12*(6+12)=216 Ватт

Или через общее сопротивление, тогда:

R_общее=(R₁*R₂)/( R₁+R₂)=(1*2)/(1+2)=2/3=0,66 Ом

I=12/0,66=18 Ампер

P=12*18=216 Ватт

Все расчёты совпали, значит найденные значения верны.

Заключение

Как вы могли убедиться найти мощность цепи или её участка совсем несложно, неважно речь идёт о постоянке или переменке. Важнее правильно определить общее сопротивление, ток и напряжение. Кстати этих знаний уже достаточно для правильного определения параметров схемы и подбора элементов – на сколько ватт подбирать резисторы, сечения кабелей и трансформаторов. Также будьте внимательны при расчёте S полной при вычислении подкоренного выражения. Стоит добавить лишь то, что при оплате счетов за коммунальные услуги мы оплачиваем за киловатт-часы или кВт/ч, они равняются количеству мощности, потребленной за промежуток времени. Например, если вы подключили 2 киловаттный обогреватель на пол часа, то счётчик намотает 1 кВт/ч, а за час – 2 кВт/ч и так далее по аналогии.

Напоследок рекомендуем просмотреть полезное видео по теме статьи:

Также читают:

• Как определить потребляемую мощность приборов
• Как рассчитать сечения кабеля
• Маркировка резисторов по мощности и сопротивлению

Основные электротехнические формулы.

Мощность. Сопротивление. Ток. Напряжение. Закон Ома. Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома. Поделиться:

Вы сейчас находитесь в каталоге:    Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.

Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления) Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока. P = мощность (Ватт) U = напряжение (Вольт) I = ток (Ампер) R = сопротивление (Ом) r = внутреннее сопротивление источнка ЭДС ε = ЭДС источника Тогда для всей цепи: I=ε/(R +r) — закон Ома для всей цепи. И еще ниже куча формулировок закона Ома для участка цепи :

Электрическое напряжение: U = R* I — Закон Ома для участка цепи U = P / I U = (P*R)1/2 Электрическая мощность: P= U* I P= R* I2 P = U 2/ R Электрический ток: I = U / R I = P/ E I = (P / R)1/2 Электрическое сопротивление: R = U / I R = U 2/ P R = P / I2 НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения. Цепь переменного синусоидального тока c частотой ω. Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты. Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала. Закон Ома для цепей переменного тока: U=I*Z где: Естественно, применительно к цепям переменного тока можно говорить и об активной/реактивной мощности. U = U0e iωt  напряжение или разность потенциалов, I  сила тока, Z = Re—iφ  комплексное сопротивление (импеданс) R = (Ra2+Rr2)1/2  полное сопротивление, Rr = ωL — 1/ωC  реактивное сопротивление (разность индуктивного и емкостного), Rа  активное (омическое) сопротивление, не зависящее от частоты, φ = arctg Rr/Ra — сдвиг фаз между напряжением и током.

19.4 Электроэнергия | Техасский шлюз

Цели обученияПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Дать определение электрической мощности и описать уравнение электрической мощности
• Расчет электрической мощности в цепях резисторов, соединенных последовательно, параллельно и комплексно

Основные термины раздела

электроэнергия

Энергия у многих ассоциируется с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядными примерами электроснабжения. Мы также используем электроэнергию, чтобы заводить автомобили, компьютеры или освещать дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.

Для начала давайте подумаем об лампочках, которые часто характеризуются номинальной мощностью в ваттах. Сравним лампочку мощностью 25 Вт с лампочкой мощностью 60 Вт (см. рис. 19.23). Хотя оба работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходная мощность электрической цепи определяется не напряжением, а чем-то иным.

Лампы накаливания, такие как две, показанные на рис. 19.23, по существу представляют собой резисторы, которые нагреваются, когда через них проходит ток, и нагреваются настолько, что излучают видимый и невидимый свет. Таким образом, две лампочки на фотографии можно рассматривать как два разных резистора. В простой цепи, такой как лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, как и напряжение, должен определять мощность.

Рис. 19.23 Слева — лампочка мощностью 25 Вт, справа — лампочка мощностью 60 Вт. Почему их выходная мощность различна, несмотря на то, что они работают на одном и том же напряжении?

Формулу мощности можно найти с помощью размерного анализа. Рассмотрим единицы мощности. В системе СИ мощность выражается в ваттах (Вт), что представляет собой энергию в единицу времени, или Дж/с

19,47 Вт=Джс.Вт=Джс.

Вспомним теперь, что напряжение — это потенциальная энергия на единицу заряда, а это означает, что единицы напряжения составляют Дж/Кл

19.48В=JC.V=JC.

Мы можем переписать это уравнение как J=V×CJ=V×C и подставить его в уравнение для ватт, чтобы получить

W=Js=V×Cs=V×Cs.W=Js=V×Cs=V ×Сс.

Но кулон в секунду (Кл/с) — это электрический ток, который мы можем видеть из определения электрического тока, I=ΔQΔtI=ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или

Р=IV. Р=IV.

Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .

Например, рассмотрим схему на рис. 19.24. По закону Ома ток, протекающий через цепь, равен

19,49I=VR=12 В100 Ом=0,12 A.I=VR=12 В100 Ом=0,12 А. VI=(12 В)(0,12 А)=1,4 Вт.P=VI=(12 В)(0,12 А)=1,4 Вт.

Куда уходит эта мощность? В этой схеме мощность идет в основном на нагрев резистора в этой цепи.

Рис. 19.24 Простая схема, потребляющая электроэнергию.

При расчете мощности в цепи на рис. 19.24 мы использовали сопротивление и закон Ома для определения силы тока. Закон Ома дает ток: I=V/RI=V/R, который мы можем подставить в уравнение для электрической мощности, чтобы получить

P=IV=(VR)V=V2RP.P=IV=(VR)V= В2Р.

Мощность определяется только напряжением и сопротивлением.

Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только через ток и сопротивление. Если мы запишем закон Ома как V=IRV=IR и используйте это, чтобы устранить V в уравнении P=IVP=IV получаем

P=IV=I(IR)=I2R.P=IV=I(IR)=I2R.

Мощность определяется только током и сопротивлением.

Таким образом, комбинируя закон Ома с уравнением P=IVP=IV для электрической мощности, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электроэнергию, либо отдают ее обратно в цепь.

Чтобы понять, как связаны между собой напряжение, сопротивление, ток и мощность, рассмотрите рис. 19.25, на котором показано колесо формул . Величины в центральной четверти окружности равны количествам в соответствующей внешней четверти окружности. Например, чтобы выразить потенциал V через мощность и ток, мы видим из круга формул, что V=P/IV=P/I.

Рис. 19.25 Колесо формул показывает, как соотносятся вольты, сопротивление, ток и мощность. Количества во внутренних четвертях кругов равны количествам в соответствующих внешних четвертях кругов.

Рабочий пример

Найдите сопротивление лампочки

Типичная старая лампочка накаливания имела мощность 60 Вт. Если предположить, что на лампочку подается напряжение 120 В, какова сила тока через лампочку?

СТРАТЕГИЯ

Нам известны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P=IVP=IV, чтобы найти ток I , протекающий через лампочку.

Решение

Решение P=IVP=IV для тока и подстановка заданных значений напряжения и мощности дает

19,51P=IVI=PV=60 W120 V=0,50 A.P=IVI=PV=60 W120 V=0,50 A.

Обсуждение

Это значительный ток. Напомним, что бытовая электроэнергия является переменным, а не постоянным током, поэтому 120 В, подаваемые из бытовых розеток, представляют собой переменную, а не постоянную мощность. 120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.

Пример работы

Грелки для ботинок

Чтобы согреть ботинки в холодные дни, вы решили вшить в стельку ботинок схему с несколькими резисторами. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите питать их от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление должно быть в каждой стельке?

СТРАТЕГИЯ

Мы знаем желаемую мощность и напряжение (18 В, потому что у нас есть две 9-вольтовые батареи, соединенные последовательно), поэтому мы можем использовать уравнение P=V2/RP=V2/R, чтобы найти необходимое сопротивление .

Решение

Решая P=V2/RP=V2/R для сопротивления и подставляя данные напряжения и мощности, мы получаем

19,52P=V2RR=V2P=(18 V)210 W=32 Ω.P=V2RR =V2P=(18 В)210 Вт=32 Ом.

Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ом.

Обсуждение

Давайте посмотрим, какой ток будет проходить по этой цепи. К сопротивлению 32 Ом приложено напряжение 18 В, поэтому закон Ома дает0003

Все аккумуляторы имеют этикетки, на которых указано, сколько заряда они могут обеспечить (в пересчете на ток, умноженный на время). Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч. (таким образом, две батареи 9 В обеспечивают 1130 мА⋅чмА⋅ч), поэтому эта система отопления будет работать в течение времени

19,54t=1130×10−3 A⋅ч0,56 A=2,0 ч.t=1130×10−3 А⋅ч0,56 А=2,0 ч.

Рабочий пример

Мощность через ветвь цепи

Сопротивление каждого резистора в схеме ниже составляет 30 Ом. Какая мощность рассеивается на средней ветви цепи?

СТРАТЕГИЯ

Средняя ветвь схемы содержит последовательно соединенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем с помощью P=V2/RP=V2/R найдем мощность, рассеиваемую в ветви.

Решение

Эквивалентное сопротивление равно Rmiddle=R3+R5=30 Ω+30 Ω=60 ΩRmiddle=R3+R5=30 Ω+30 Ω=60 Ω. Мощность, рассеиваемая средней ветвью цепи, составляет

19,55Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.

Обсуждение

Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, выдаваемой батареей. Во-первых, эквивалентное сопротивление левой ветви равно

19,56Rleft=11/R1+1/R2+R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом.Rleft=11/R1+1/R2 +R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом.

Мощность через левую ветвь равна

19,57Pleft=V2Rleft=(12 В)245 Ом=3,2Вт. Pleft=V2Rleft=(12 В)245 Ом=3,2 Вт. эквивалентное сопротивление равно Rright=R6=30 ΩRright=R6=30 Ω. Мощность через правую ветвь равна

19,58Pright=V2Rright=(12 В)230 Ом=4,8Вт.Pright=V2Rright=(12 В)230 Ом=4,8 Вт

Полная мощность, рассеиваемая цепью, представляет собой сумму мощностей, рассеиваемых в каждой ветви .

19.59P=Pleft+Pmiddle+Pright=2.4 W+3.2 W+4.8 W=10.4 WP=Pleft+Pmiddle+Pright=2.4 W+3.2 W+4.8 W=10.4 Вт

Мощность батареи

19.60P=IV.P=IV.

, где I — общий ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить я . Ответвления вносят токи

19,61Ileft=VRleft=12 V45 Ω=0,2667 AImiddle=VRmiddle=12 V60 Ω=0,20 AIright=VRright=12 V30 Ω=0,40 A.Ileft=VRleft=VRleft=12 V05 6Ω=6Ω 12 V60 Ом=0,20 AIright=VRright=12 V30 Ω=0,40 A. =0,2667 A+0,20 A+0,40 A=0,87 A.

и мощность, обеспечиваемая аккумулятором, составляет

19,63P=IV=(0,87 A)(12 В)=10,4 W. P=IV=(0,87 A)(12 В)=10,4 Вт.

Это та же мощность, которая рассеивается на резисторах цепи, что показывает сохранение энергии в этой цепи.

Практические задания

Какова формула мощности, рассеиваемой на резисторе?

1. Формула мощности, рассеиваемой на резисторе: P=IV.P=IV.
2. Формула для мощности, рассеиваемой на резисторе: P=VI.P=VI.
3. Формула для мощности, рассеиваемой на резисторе: P = IV .
4. Формула для мощности, рассеиваемой на резисторе: P = I ² В .

Какова формула для мощности, рассеиваемой резистором, при заданном его сопротивлении и напряжении на нем?

1. Формула мощности, рассеиваемой на резисторе: P=RV2P=RV2
2. Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
3. Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
4. Формула для мощности, рассеиваемой на резисторе: P=I2RP=I2R

Проверьте свое понимание

Упражнение 8

Какие элементы схемы рассеивают мощность?

1. конденсаторы
2. катушки индуктивности
3. идеальные переключатели
4. резисторы

Упражнение 9

Объясните словами уравнение для мощности, рассеиваемой на данном сопротивлении.

1. Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.
2. Электрическая мощность пропорциональна квадрату тока через резистор, умноженному на напряжение на резисторе.
3. Электрическая мощность пропорциональна току через резистор, деленному на напряжение на резисторе.
4. Электрическая мощность пропорциональна току через резистор, умноженному на напряжение на резисторе.

• Печать
• Поделиться

Напряжение, ток, сопротивление и закон Ома

• Дом
• Учебники
• Напряжение, ток, сопротивление и закон Ома

≡ Страниц

Авторы: CTaylor

Избранное Любимый 135

Основы электричества

Приступая к изучению мира электричества и электроники, очень важно начать с понимания основ напряжения, силы тока и сопротивления. Это три основных строительных блока, необходимых для управления электричеством и его использования. Поначалу эти концепции может быть трудно понять, потому что мы не можем их «видеть». Нельзя невооруженным глазом увидеть энергию, текущую по проводу, или напряжение батареи, лежащей на столе. Даже молния в небе, хотя и видимая, на самом деле является не обменом энергией, происходящим от облаков к земле, а реакцией воздуха на проходящую через него энергию. Чтобы обнаружить эту передачу энергии, мы должны использовать инструменты измерения, такие как мультиметры, анализаторы спектра и осциллографы, чтобы визуализировать то, что происходит с зарядом в системе. Не бойтесь, однако, этот учебник даст вам общее представление о напряжении, токе и сопротивлении и о том, как они связаны друг с другом.

Георг Ом

Описано в этом руководстве

• Как электрический заряд связан с напряжением, током и сопротивлением.
• Что такое напряжение, ток и сопротивление.
• Что такое закон Ома и как с его помощью понять электричество.
• Простой эксперимент для демонстрации этих концепций.

Рекомендуемая литература

• Что такое электричество
• Что такое цепь?

Электрический заряд

Электричество — это движение электронов. Электроны создают заряд, который мы можем использовать для совершения работы. Ваша лампочка, ваша стереосистема, ваш телефон и т. д. используют движение электронов для выполнения работы. Все они работают, используя один и тот же основной источник энергии: движение электронов.

Три основных принципа этого руководства можно объяснить, используя электроны, или, точнее, создаваемый ими заряд:

• Напряжение — это разница заряда между двумя точками.
• Ток — скорость, с которой течет заряд.
• Сопротивление — это способность материала сопротивляться потоку заряда (току).

Итак, когда мы говорим об этих значениях, мы на самом деле описываем движение заряда и, таким образом, поведение электронов. Цепь представляет собой замкнутый контур, который позволяет заряду перемещаться из одного места в другое. Компоненты в цепи позволяют нам контролировать этот заряд и использовать его для выполнения работы.

Георг Ом был баварским ученым, изучавшим электричество. Ом начинается с описания единицы сопротивления, которая определяется током и напряжением. Итак, давайте начнем с напряжения и пойдем оттуда.

Напряжение

Мы определяем напряжение как количество потенциальной энергии между двумя точками цепи. Одна точка имеет больший заряд, чем другая. Эта разница заряда между двумя точками называется напряжением. Он измеряется в вольтах, что технически представляет собой разность потенциалов между двумя точками, которые передают один джоуль энергии на кулон проходящего через них заряда (не паникуйте, если это не имеет смысла, все будет объяснено). Единица «вольт» названа в честь итальянского физика Алессандро Вольта, который изобрел то, что считается первой химической батареей. Напряжение обозначается в уравнениях и схемах буквой «V».

При описании напряжения, тока и сопротивления часто используется аналогия с резервуаром для воды. В этой аналогии заряд представлен количеством воды , напряжение представлен давлением воды , а ток представлен потоком воды . Итак, для этой аналогии запомните:

• Вода = Зарядка
• Давление = Напряжение
• Расход = Текущий

Рассмотрим резервуар для воды на определенной высоте над землей. На дне этого бака есть шланг.

Давление на конце шланга может представлять собой напряжение. Вода в баке представляет собой заряд. Чем больше воды в баке, тем выше заряд, тем большее давление измеряется на конце шланга.

Мы можем думать об этом резервуаре как о батарее, месте, где мы храним определенное количество энергии, а затем высвобождаем ее. 18 электронов (1 кулон) в секунду, проходящих через точку цепи. Усилители представлены в уравнениях буквой «I».

Допустим, у нас есть два резервуара, к каждому из которых подходит шланг снизу. В каждом баке одинаковое количество воды, но шланг одного бака уже, чем шланг другого.

Мы измеряем одинаковое давление на конце любого шланга, но когда вода начинает течь, расход воды в баке с более узким шлангом будет меньше расхода воды в баке с более широким шлангом. В электрических терминах ток через более узкий шланг меньше, чем ток через более широкий шланг. Если мы хотим, чтобы поток через оба шланга был одинаковым, мы должны увеличить количество воды (зарядку) в баке с более узким шлангом.

Это увеличивает давление (напряжение) на конце более узкого шланга, проталкивая больше воды через бак. Это аналогично увеличению напряжения, которое вызывает увеличение тока.

Теперь мы начинаем видеть взаимосвязь между напряжением и током. Но здесь следует учитывать третий фактор: ширину шланга.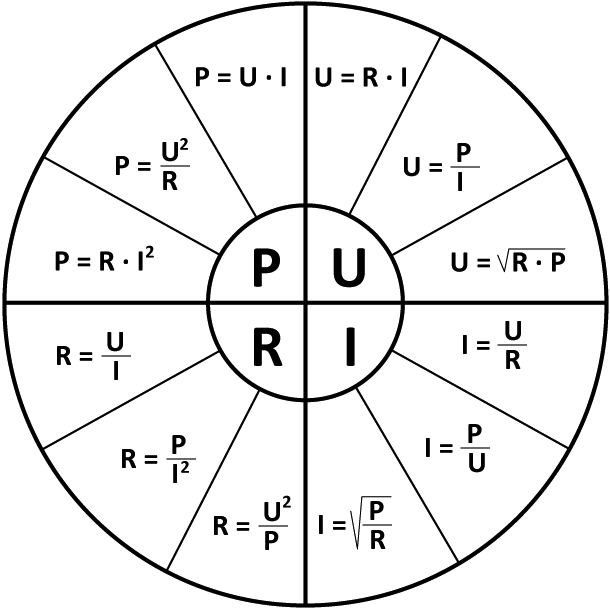 В этой аналогии ширина шланга является сопротивлением. Это означает, что нам нужно добавить еще один член в нашу модель:

• Вода = заряд (измеряется в кулонах)
• Давление = Напряжение (измеряется в вольтах)
• Расход = ток (измеряется в амперах или сокращенно «Амперах»)
• Ширина шланга = сопротивление

Сопротивление

Рассмотрим еще раз наши два резервуара для воды, один с узкой трубой, а другой с широкой трубой.

Само собой разумеется, что мы не можем пропустить через узкую трубу такой же объем, как через более широкую при том же давлении. Это сопротивление. Узкая труба «сопротивляется» потоку воды через нее, хотя вода находится под тем же давлением, что и резервуар с более широкой трубой. 918 электронов. Это значение обычно обозначается на схемах греческой буквой «Ω», которая называется омега и произносится как «ом».

Закон Ома

Объединив элементы напряжения, тока и сопротивления, Ом вывел формулу:

Где

• В = напряжение в вольтах
• I = ток в амперах
• R = сопротивление в омах

Это называется законом Ома.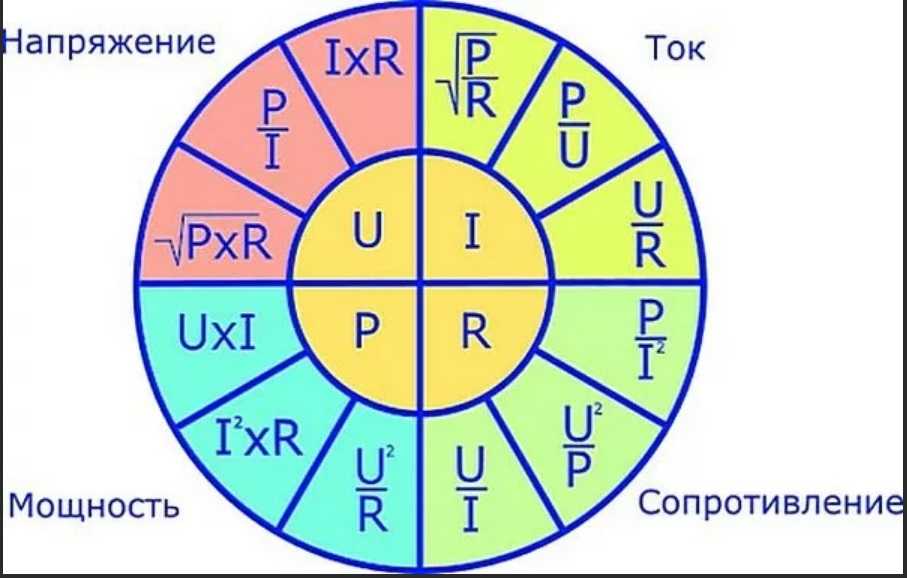 Допустим, например, что у нас есть цепь с потенциалом 1 вольт, током 1 ампер и сопротивлением 1 Ом. Используя закон Ома, мы можем сказать:

Допустим, это наш бак с широким шлангом. Количество воды в баке определяется как 1 вольт, а «узость» (сопротивление течению) шланга определяется как 1 Ом. Используя закон Ома, это дает нам поток (ток) в 1 ампер.

Используя эту аналогию, давайте теперь посмотрим на бак с узким шлангом. Поскольку шланг уже, его сопротивление потоку выше. Определим это сопротивление как 2 Ом. Количество воды в резервуаре такое же, как и в другом резервуаре, поэтому, используя закон Ома, наше уравнение для резервуара с узким шлангом равно 9.0003

Но какой ток? Поскольку сопротивление больше, а напряжение такое же, это дает нам значение тока 0,5 ампер:

Итак, в баке с большим сопротивлением ток меньше. Теперь мы можем видеть, что если мы знаем два значения закона Ома, мы можем найти третье. Продемонстрируем это на эксперименте.

Эксперимент по закону Ома

В этом эксперименте мы хотим использовать 9-вольтовую батарею для питания светодиода. Светодиоды хрупкие, и через них может протекать только определенное количество тока, прежде чем они сгорят. В документации на светодиод всегда будет «номинальный ток». Это максимальное количество тока, которое может протекать через конкретный светодиод, прежде чем он перегорит.

Необходимые материалы

Для проведения экспериментов, перечисленных в конце руководства, вам понадобятся:

• Мультиметр
• Батарея 9 В
• Резистор 560 Ом (или следующее ближайшее значение)
• Светодиод

ПРИМЕЧАНИЕ. Светодиоды известны как «неомические» устройства. Это означает, что уравнение для тока, протекающего через сам светодиод, не так просто, как V=IR. Светодиод вносит в цепь то, что называется «падением напряжения», тем самым изменяя величину тока, протекающего через нее. Однако в этом эксперименте мы просто пытаемся защитить светодиод от перегрузки по току, поэтому мы пренебрежем токовыми характеристиками светодиода и выберем значение резистора, используя закон Ома, чтобы быть уверенным, что ток через светодиод безопасно ниже 20 мА.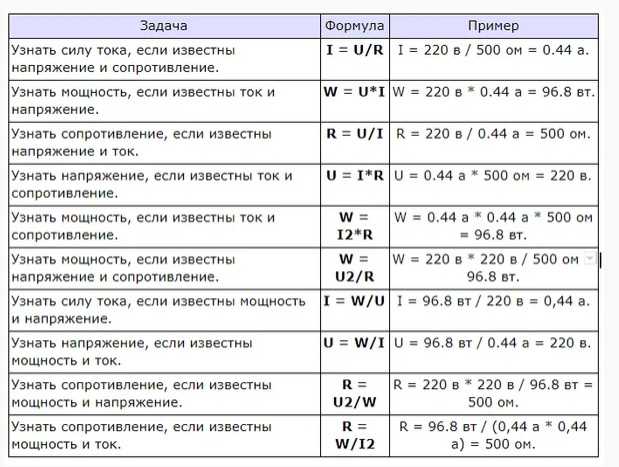

В этом примере у нас есть 9-вольтовая батарея и красный светодиод с номинальным током 20 миллиампер или 0,020 ампер. Чтобы быть в безопасности, мы бы предпочли не управлять светодиодом с его максимальным током, а предпочесть рекомендуемый ток, который указан в его спецификации как 18 мА или 0,018 ампер. Если мы просто подключим светодиод непосредственно к батарее, значения для закона Ома будут выглядеть так:

, следовательно:

и, поскольку у нас еще нет сопротивления:

Деление на ноль дает нам бесконечный ток! Ну, на практике не бесконечный, а столько тока, сколько может выдать батарея. Поскольку мы НЕ хотим, чтобы через наш светодиод протекал такой большой ток, нам понадобится резистор. Наша схема должна выглядеть так:

Точно так же мы можем использовать закон Ома, чтобы определить сопротивление резистора, которое даст нам желаемое значение тока:

следовательно:

подставив наши значения:

вычислив сопротивление:

Итак, нам нужен сопротивление резистора около 500 Ом, чтобы ток через светодиод оставался ниже максимального номинального тока.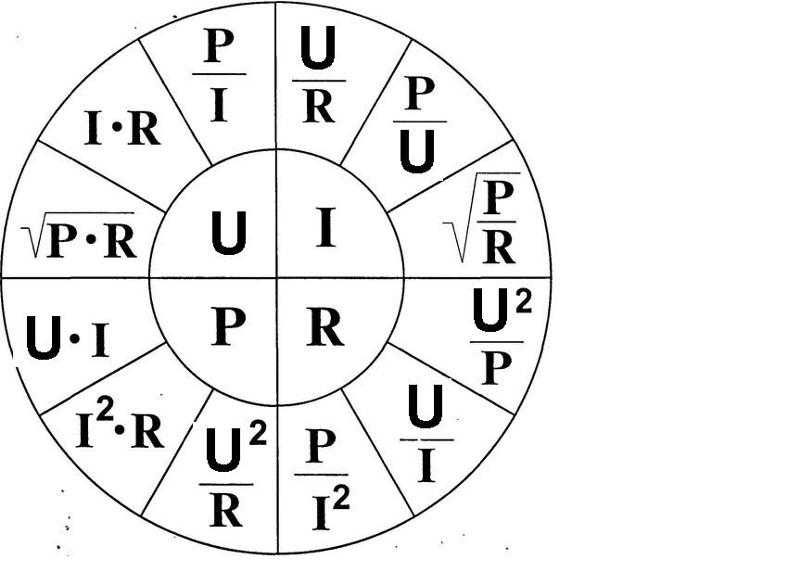

500 Ом не является обычным значением для стандартных резисторов, поэтому в этом устройстве вместо него используется резистор на 560 Ом. Вот как выглядит наше устройство в собранном виде.

Успех! Мы выбрали сопротивление резистора, достаточно высокое, чтобы ток через светодиод оставался ниже его максимального номинала, но достаточно низкое, чтобы тока было достаточно, чтобы светодиод оставался красивым и ярким.

Этот пример со светодиодом и токоограничивающим резистором часто встречается в любительской электронике. Вам часто придется использовать закон Ома, чтобы изменить величину тока, протекающего через цепь. Другой пример этой реализации можно увидеть в светодиодных платах LilyPad.

При такой настройке вместо выбора резистора для светодиода резистор уже встроен в светодиод, поэтому ограничение тока выполняется без добавления резистора вручную.

Ограничение тока до или после светодиода?

Чтобы немного усложнить ситуацию, вы можете разместить токоограничивающий резистор с любой стороны светодиода, и он будет работать точно так же!

Многие люди, впервые изучающие электронику, сомневаются в том, что токоограничивающий резистор может располагаться с любой стороны светодиода, и схема будет работать как обычно.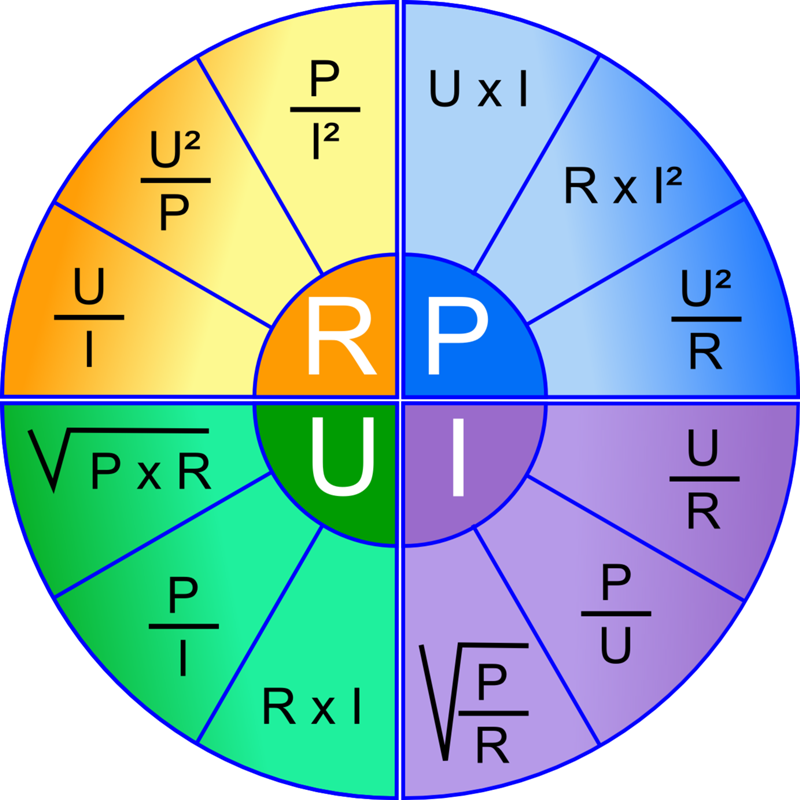

Представьте себе реку в непрерывной петле, бесконечную, круговую, текущую реку. Если бы мы поместили в нем плотину, вся река перестала бы течь, а не только один берег. Теперь представьте, что мы помещаем в реку водяное колесо, которое замедляет течение реки. Неважно, в каком месте круга находится водяное колесо, оно все равно замедлит поток на 9-м уровне.0297 вся река .

Это упрощение, так как токоограничивающий резистор не может быть размещен где-либо в цепи ; его можно разместить на с любой стороны светодиода для выполнения своей функции.

Чтобы получить более научный ответ, обратимся к закону напряжения Кирхгофа. Именно из-за этого закона токоограничивающий резистор может располагаться с любой стороны светодиода и при этом иметь тот же эффект. Для получения дополнительной информации и решения некоторых практических задач по использованию KVL посетите этот веб-сайт.

Ресурсы и дальнейшие действия

Теперь вы должны понимать, что такое напряжение, ток, сопротивление и как они связаны между собой.