| L237-101 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый мат (11 365.34 р.) | ||
| L237-100 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый бриллиант (11 365.34 р.) | ||
| L237-104 SPOT TRESIDE раковина 43 х 38 х 15 см цвет черный бриллиант (14 730.07 р.) | ||
| L237-105 SPOT TRESIDE раковина 43 х 38 х 15 см цвет черный мат (14 730.07 р.) | ||
L237-114 SPOT TRESIDE раковина 43 х 38 х 15 см цвет оранж (17 048. | ||
| L237-121 SPOT TRESIDE раковина 43 х 38 х 15 см цвет зеленый (17 048.00 р.) | ||
| L237-116 SPOT TRESIDE раковина 43 х 38 х 15 см цвет серый (17 048.00 р.) | ||
| L237-115 SPOT TRESIDE раковина 43 х 38 х 15 см цвет желтый (17 048.00 р.) | ||
| L237-113 SPOT TRESIDE раковина 43 х 38 х 15 см цвет красный (17 048.00 р.) | ||
L237-112 SPOT TRESIDE раковина 43 х 38 х 15 см цвет морская волна (17 048. 00 р.) 00 р.) | ||
| L237-108 SPOT TRESIDE раковина 43 х 38 х 15 см цвет синий (17 048.00 р.) | ||
| L237-107 SPOT TRESIDE раковина 43 х 38 х 15 см цвет шоколад (17 048.00 р.) | ||
| L237-103 SPOT TRESIDE раковина 43 х 38 х 15 см цвет пергамент (17 048.00 р.) | ||
| L237-253 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-медь (19 365.93 р.) | ||
L237-221 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-зеленый (19 365. | ||
| L237-216 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый -серый (19 365.93 р.) | ||
| L237-215 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-желтый (19 365.93 р.) | ||
| L237-214 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-оранж (19 365.93 р.) | ||
| L237-213 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-красный (19 365.93 р.) | ||
L237-212 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-морская волна (19 365. 93 р.) 93 р.) | ||
| L237-208 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-синий (19 365.93 р.) | ||
| L237-207 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-шоколад (19 365.93 р.) | ||
| L237-205 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-черный мат (19 365.93 р.) | ||
| L237-204 SPOT TRESIDE раковина 43 х 38 х 15 см цвет белый-черный бриллиант (19 365.93 р.) | ||
L237-251 SPOT TRESIDE раковина 43 х 38 х 15 см цвет платина (26 095. 41 р.) 41 р.) | ||
| L237-250 SPOT TRESIDE раковина 43 х 38 х 15 см цвет золото (31 404.22 р.) |
модно и практично в Москве
Сегодня мы представим лучшие раковины, их также называют умывальники, которые можно установить в углу ванной комнаты. Как можно догадаться, прежде всего угловая раковина станет удачным решением для небольшой, может бы даже совсем миниатюрной ванной комнаты или санузла. Все сантехнические объекты, равно как и мебель, размещаемая в малогабаритное помещение, должны подбираться с целью зрительно расширить пространство. Рекомендуем купить угловую раковину — оригинальный и хорошо смотрящийся элемент интерьера, который не зря зарекомендовал себя среди покупателей и стал очень востребованным.
Угловые умывальники — интересное предложение на сантехническом рынке, создавшее серьезную конкуренцию обыкновенным подвесным раковинам.
Цена угловой раковины зачастую ниже обычной, что логично для такой миниатюрной конструкции, при этом, изысканный дизайн подвесных раковин углового монтажа коллекций Jacob Dalafon, Laufen, Villeroy & Boch и Duravit заслуживает высочайшей оценки.
Вот некоторые вариации таких раковин.
Угловые умывальники на пьедестале, их называют
У такой установки умывальника в ванной есть единственный минус: пьедестал «крадет» место под чашей раковины, которое стоило было бы занять чем-либо более рационально.
Но раковина может располагаться у углу ванной, крепясь за две стены.
Внутренняя форма таких моделей также, предлагает многообразие форм, от треугольника до овала.
А вот версия рационального использования потенциала свободного пространства — угловая раковина, встроенная в тумбу.
Популярный материал для изготовления угловых раковин, это санфаянс, известный достаточно высокой прочностью, гладкостью поверхности и гигиеничностью.
Проанализировав особенности угловых раковин, можно резюмировать: это идеальный вариант небольших помещений, поскольку «скромно» и компактно располагается в углу ванной комнаты, тем самым высвобождая драгоценные сантиметры площади. Сюда можно поместить стиральную машину, шкафчик и так далее.
Однако, все вышесказанное это далеко не вердикт, ведь подобная раковина будет так же удачно смотреться в ванных абсолютно любых размеров и планировки.
Наконец, треугольный угловой умывальник блестяще совмещается с большинством стилей в дизайне ванных. Кроме того, сам вид угловых раковин достаточно интересен и не банален, это свежо и оригинально.
Еще один плюс такого санфаянса — надежность крепления. Большинство таких раковин углового типа имеют консольное крепление – их подвешивают на стену. Угловая модель подвесной раковины, в отличие от другой настенной держится более крепко, ведь в этом случае она держится сразу за две стены, а не одну.
10 сен. 2014 г.
4 109
Современный, нестандартный и просторный треугольные раковина
Планирование покупки долговечных, индивидуальных и высококачественных. треугольные раковина для ваших кухонь? Alibaba.com предлагает вам лучшее качество. треугольные раковина, которые идеально подходят для всех видов использования, включая домашнее и коммерческое использование, по выгодным ценам и по выгодным ценам. Файл. треугольные раковина на сайте просторны и изготовлены из высококачественных материалов, таких как нержавеющая сталь, мрамор, гранит и многие другие.Покупайте у самых известных и ведущих продавцов и поднимите полезность мойки на новый уровень.
треугольные раковина очень важны для любого типа кухни и могут использоваться для бесчисленного множества целей, начиная от мытья посуды и заканчивая мытьем продуктов и многого другого. Следовательно, ваш. треугольные раковина всегда должен быть просторным и удобным, чтобы поместиться в любую посуду, и достаточно глубоким, чтобы не пропускать воду во время уборки. Последний. Коллекции треугольные раковина на сайте идеально подходят для любой кухни, большой или маленькой, и имеют одно или два отверстия.
Широкая коллекция. треугольные раковина на Alibaba.com доступен в различных формах, размерах, дизайне и различных качествах материалов, из которых вы можете выбирать. Эти. треугольные раковина просты в установке и могут быть прикреплены к столешнице на кухне. Вы можете выбирать из множества. треугольные раковина по толщине и длине, и они составляют эффективную сушильную доску, что делает их идеальными для кухни ресторана.
Вы можете выбрать вариант с краном или без него, в зависимости от того, что вам больше подходит.
Получите экономию. треугольные раковина на Alibaba.com и прекратите тратить лишние деньги на покупку эффективных продуктов. Доступны заказы OEM, и вы также можете настроить продукцию в соответствии с вашими требованиями. Закажите их сейчас и наслаждайтесь блестящими предложениями.
размеры треугольных умывальников в угол с пьедесталом, на стойке или подвесной установки в маленькой комнате
Экономия пространства без потери практического значения – угловые модели моек. Но желаемый результат возможен только при правильном выборе модели.
Уголовная мойка: комфорт на кухне
Угловые модели моек отвечают многим запросам потребителей – от привлекательного внешнего вида до практичности изделия.
Размеры, формы, установка – настолько разнообразные, что перед покупкой стоит изучить ассортимент, представленный производителями.
Преимущества применения угловой раковины
Угловые раковины перед другими альтернативами имеют ряд преимуществ:
- Компактно, аккуратно смотрится в ванной комнате и подходит для помещения с небольшими габаритами.

- Преобразует любой угол с коммуникациями, создав функциональную зону.
- Изделия представлены разной формы и конфигурации, с дополнительными отсеками бортиками для комфорта.
Единственным недостатком может показаться размещение в углу, кому-то неудобно стоять и мыть в таком положении посуду, но в действительности аргументов «за» куда больше.
Какие бывают угловые раковины?
Производители предлагают широкий ассортимент продукции разной формы, материалов. Выбор напрямую зависит от личных предпочтений и особенностей кухни.
По использованию материала
- Акриловые изделия экологичные, практичные и гладкие на ощупь. Такие мойки отличаются стильным дизайном, поэтому подойдут под любой интерьер.
- Наиболее доступным и практичным вариантом остаются модели из нержавеющей стали. Они абсолютно не прихотливы в уходе и прослужат долгие годы. Металлические мойки – стальные или медные, хорошо смотрятся в кухне с классическим интерьером, что присуще многим домам.

- Мраморные изделия самые дорогие, к ним же приравниваются керамические изделия. Вложения в такие материалы оправдывают себя, ведь они служат не один десяток лет и выглядят привлекательно несмотря на срок эксплуатации. Стойко переносят механические повреждения. Органично смотрятся изделия в скандинавском и английском стилях.
По размерам
Минимальный показатель ширины составляет 30 см. производители предлагают варианты – 37, 49, 50 см, выбор напрямую зависит от предпочтений и особенностей помещения. А вот второй параметр – составляет 45, 47, 50, 57 см.
По форме и статистике
Популярные формы угловых моек – круглая или овальная. Куда удобнее мыть кастрюли в круглых формах. Современные кухни комплектуются чашами с двумя емкостями – круглой для посуды и квадратной для овощей. Менее популярными остаются квадратные и трапециевидные модели.
Глубина чаши может варьироваться от 16-20 см. Выбор напрямую зависит от посуды, которой постоянно пользуется семья.
Выбор в пользу классической глубины 20-22 см позволит удобно приготовить и убрать на кухне. Минимальное расстояние столешницы перед раковиной составляет 5 см.
По типу установки
- Изделие устанавливается на столешницу, опираясь бортиками на нее.
- Врезные варианты, фиксируются просто в заранее сделанное отверстие в столешнице.
- Формы тюльпан опираются на специальные подставки.
- Интегрированные мойки создаются на фабриках и выглядят как продолжение столешницы.
- Умывальники с комодом требует предварительного сопоставления всех элементов шкафа.
Какие стандартные размеры углового умывальника?
Современный рынок предлагает потребителям широкий выбор моделей разных размеров. Самая маленькая модель 30×30 см, но она самая неудобная. В идеале подобрать модель кратную 50 см. Если раковина идет в комплекте с тумбой, то стоит обратить внимание на модели параметрами 35-70х35-70 см.
Где может применяться умывальник в угол?
Угловой умывальник – идеальное решение для маленьких ванных комнат.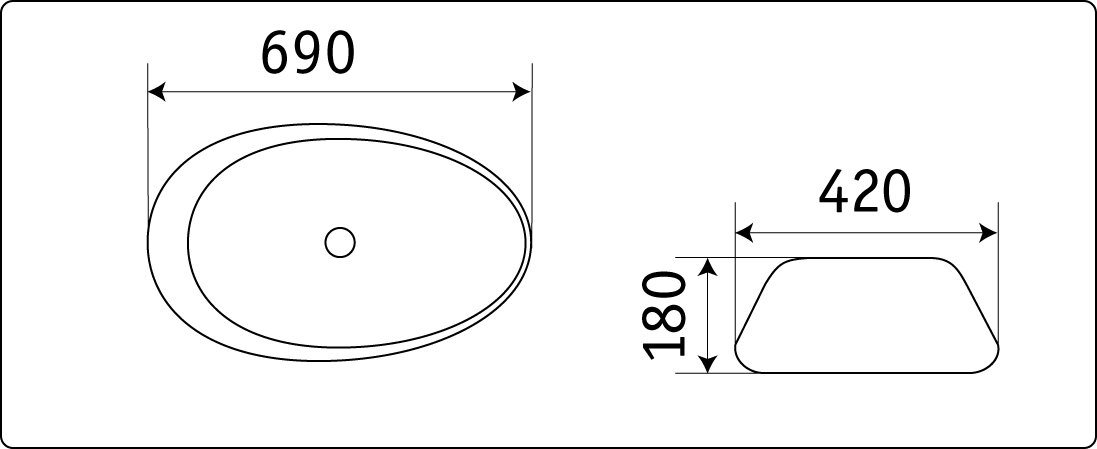 Такая раковина устанавливается для мытья рук и в общественных местах.
Такая раковина устанавливается для мытья рук и в общественных местах.
Не менее практичным решением будет такая мойка в кухне, но тогда подбираются максимально возможные параметры. Угловая модель станет прекрасным дополнением ванной комнаты.
Асимметричные модели – идеальное решение для помещения с непропорциональными углами.
Как происходит установка?
Основные технологические моменты установки:
- Сборка основного элемента и крепежных составляющих.
- Монтаж смесителя и сифона.
- Подключение коммуникаций.
В остальном нюансы установки зависят от особенностей конструкции — с пьедесталом или с комодом.
Пространство не должно быть потеряно за счет создания «глухих» или труднодоступных ящиков
С пьедесталом
- Проведите подготовительные работы поверхности – пол должен быть ровным.
- Чтобы установить все ровно, сделайте отметки под места крепления и проведите между ними линию. Точность измерений подтвердит монтажный уровень.

- В отмеченных местах делаем отверстия с помощью перфоратора или дрели.
- Отверстия заполняются клеем, закрепляются распорные дюбеля.
- Вкручиваются саморезы, мойка закрепляется.
- Раковина на пьедестале размещается так, чтобы выемки для слива находились по центру.
- Мойка фиксируется на поверхности стены, но гайки затягиваются не туго, чтобы изделие не треснуло. Декоративные заглушки используются, чтобы скрыть гайки. Мойка должна быть устойчивой.
- Устанавливается сифон и только потом смеситель.
Большой умывальник с комодом
- Сначала собирается комод, затем производится его установка.
- После регулировки опор, примеряется чаша.
- Для крепления тумбы, а потом раковины предстоит нанести разметки для создания отверстий.
- В стене делаются отверстия, устанавливается шкафчик.
- Завершающий этап – установка сифона и смесителя.
Чтобы бортики хорошо прилегали к стене, рекомендуется использовать силикон. Мойка хорошо прижимается к торцам, чтобы герметик застыл. Процедура позволяет зафиксировать емкость и уберечь тумбу от попадания воды.
Мойка хорошо прижимается к торцам, чтобы герметик застыл. Процедура позволяет зафиксировать емкость и уберечь тумбу от попадания воды.
Маленькая мойка в ванную комнату или кухню
В ванную комнату можно установить самую маленькую модель 30 на 30, но она подойдет только для мытья рук.
На рынке представлен широкий выбор миниатюрных умывальников с удобной тумбой. Значительным спросом пользуется навесной вариант с зеркалом, который можно дополнить бра, стильными светильниками. А вот для кухни идеальное решение – умывальных встроенный в столешницу или тумбу.
Советы и рекомендации
Первоначальный вид и лоск раковины сохранится при бережном отношении к изделию:
- Не помещайте в раковину ничего тяжелого, чтобы не перегрузить ее, а также избежать механических повреждений.
- Чтобы она не засорилась, не бросайте в мойку куски полиэтилена, волосы.
- Особенности ухода напрямую зависят материала изделия. Если это стекло, то поверхность всегда вытирается насухо, чтобы не было разводов.
 Керамика очищается раз в 7 дней с помощью кислотосодержащих или простых средств. Изделия из натурального камня очищаются специальными средствами, мягкими губками, салфетками. Пастообразными, гелевыми чистящими составами. Очищаются искусственные покрытия и приводятся до блеска.
Керамика очищается раз в 7 дней с помощью кислотосодержащих или простых средств. Изделия из натурального камня очищаются специальными средствами, мягкими губками, салфетками. Пастообразными, гелевыми чистящими составами. Очищаются искусственные покрытия и приводятся до блеска. - Подбирая раковину, обратите внимание на наличие переливного отверстия. Клапан должен идти в комплекте, ведь потом тяжело подобрать подходящий вариант по существующим параметрам.
- Уточните у продавца комплектацию раковины, предусмотрен ли сифон или его придется приобретать отдельно.
- Подбирайте изделие с учетом дизайна комнаты, стиля другой сантехники.
- Изучите параметры помещения, габариты самого изделия.
Угловые модели созданы, чтобы обеспечить максимальный комфорт для хозяйки на кухне, а также сэкономить рабочее пространство. Разнообразие моделей и форм приятно удивит любого потребителя.
Полезное видео
Треугольные, прямоугольные, круглые раковины для ванной: разбираемся во всем разнообразии
Казалось бы, раковина – такая незначительная деталь, и проблем с ее выбором возникнуть не должно. Но на практике оказывается иначе: только представьте, с каким разнообразием предложенных моделей вы столкнетесь в любом более-менее крупном магазине сантехники, не говоря уж о многочисленных страницах виртуальной площадки.
Но на практике оказывается иначе: только представьте, с каким разнообразием предложенных моделей вы столкнетесь в любом более-менее крупном магазине сантехники, не говоря уж о многочисленных страницах виртуальной площадки.
Сегодня мы рассмотрим все тонкости выбора раковины для ванной комнаты, в частности, разберемся, какой форме отдать предпочтение, какому материалу и конструкции.
Содержание:
Треугольные, квадратные или круглые раковины для ванной?
Чаще всего в магазинах можно встретить раковины следующих форм:
- круглые
- прямоугольные
- треугольные (угловые)
А пока рассмотрим основные преимущества той или иной стандартной формы.
Так, круглые раковины – это вечная классика, которая будет уместна в интерьере любой стилистической направленности. Они идеально впишутся как в классический интерьер, так и в более современный.
Что же касается прямоугольных раковин, то они будут наиболее уместными в сдержанных строгих интерьерах. И конечно же, без них дело не обойдется в современном минимализме, лофте, гранже. Словом, во всех стилях, в которых больше всего ценится простота и незамысловатость форм, четкость линий и функциональность.
Треугольная раковина, которую можно установить в угол комнаты, несомненно выигрышный вариант для маленькой ванной комнаты, где каждый сантиметр свободного пространства на счету. Почему бы не сохранить немного пространства, установив небольшую треугольную раковину, которая займет совсем немного места в углу и будет ничуть не менее удобной, нежели полноразмерый круглый либо прямоугольный вариант?
Какой конструкции отдать предпочтение?
- Тюльпан.
 Стандартная раковина «на ножке», основным достоинством которой можно считать не только функциональность, но и эстетику. Что ж, действительно, самое достойное решение для габаритной ванной в классическом стиле.
Стандартная раковина «на ножке», основным достоинством которой можно считать не только функциональность, но и эстетику. Что ж, действительно, самое достойное решение для габаритной ванной в классическом стиле. - Кувшинка. Еще одно «цветочное» название, точно описывающее раковину без «ножки». Ввиду такой конструкции расположить ее можно над каким-либо другим элементом обстановки, чаще всего, над стиральной машиной. Такие раковины выбирают владельцы небольших квартир с крохотными ванными.
- Классическая подвесная раковина. Конструктивно данная разновидность также подразделяется на два типа. Речь идет о раковинах, где присутствует отдельное отверстие для смесителя и где таковое отсутствует. Последний вариант будет пригодным, если вы решили по-старинке оставить в комнате всего один смеситель с длинным изливом, однако если для вас куда важнее комфорт, чем стоимость раковины, отдайте предпочтение модели с отверстием для излива.
- Встроенные конструкции. Крайне эстетичные, функциональные и при этом дорогостоящие.
 Для их установки потребуется приобретение специального шкафчика, так называемого мойдодыра, в который встроено зеркало. К слову, шкафчик можно использовать не только для хранения бытовых мелочей, но и для того, чтобы скрыть все неприглядные коммуникации.
Для их установки потребуется приобретение специального шкафчика, так называемого мойдодыра, в который встроено зеркало. К слову, шкафчик можно использовать не только для хранения бытовых мелочей, но и для того, чтобы скрыть все неприглядные коммуникации. - Мини-раковины. По сути, обыкновенная конструкция, отличающаяся от полноразмерного варианта лишь более скромными габаритами.
- Накладные раковины – новое слово в сантехнике. Как следует из названия, ее можно просто положить на специальную столешницу и спокойно расставлять на последней разные мелочи и даже бытовые приборы, а под столешницей расположить стиральную машину. Это совершенно безопасно, так как конструкция раковины полностью исключает протечки воды.
Все внимание материалу
Наиболее распространенным материалом изготовления раковин и прочей сантехники является керамика. Это понятие объединяет в себе две разновидности материалов:
- Фаянс. Материал самый доступный, однако малопрактичный.
 Его поверхность недостаточно гладкая и слишком пористая, ввиду чего материал сильно подвержен окрашиваю и страдает от малейших механических повреждений.
Его поверхность недостаточно гладкая и слишком пористая, ввиду чего материал сильно подвержен окрашиваю и страдает от малейших механических повреждений. - Фарфор. Куда более дорогостоящий, но надежный. Его структура имеет меньшее количество пор и в целом более гладкая.
Куда меньшим спросом пользуется натуральный мрамор, что обуславливается не только его высокой ценой, но и непрактичностью. Также раковины изготавливаются из современных материалов, к примеру, стали и специального высокопрочного стекла.
Смотрите, как выбирать раковину, на видео:
Анатомия ушных раковин | Александр Маркушин пластический хирург
Наружное ухо состоит из ушной раковины и слухового канала. Ушная раковина направляет звуковые волны из окружающей среды через слуховой канал к барабанной перепонке. Эта извилистая, похожая на оболочку гибкая структура, является функционально важной. Отклонения от нормы или отклонения в положении, форме, размере или архитектуре ушной раковины заметны и нежелательны. Тщательная хирургическая коррекция или реконструкция могут восстановить красоту уха и гармоничный внешний вид с лицом.
Ушная раковина направляет звуковые волны из окружающей среды через слуховой канал к барабанной перепонке. Эта извилистая, похожая на оболочку гибкая структура, является функционально важной. Отклонения от нормы или отклонения в положении, форме, размере или архитектуре ушной раковины заметны и нежелательны. Тщательная хирургическая коррекция или реконструкция могут восстановить красоту уха и гармоничный внешний вид с лицом.
Техника эстетической отопластики элегантна и часто сложна и основана на полном понимании анатомии. Наряду с знанием мышц, нервов и сосудов, кровоснабжающих ушную раковину, каждая складка, вогнутость и выпуклость уха должны быть четко запечатлены в сознании любого пластического хирурга, приступающего к эстетической отопластике и реконструкции ушной раковины.
Ушная раковина
Ушная раковина представляет собой часть наружного уха неправильной формы, которая выступает в стороны на уровне височной кости.
Ушная раковина состоит из упругой извилистой хрящевой пластинки, покрытой кожей. Ушная раковина немного наклонена назад, так что длинная ось создает угол около 8 ° с позадичелюстной (ретромандибулярной) линией. Верхняя часть ушной раковины расположена в вертикальной плоскости на одном уровне с бровью. Нормальное отстояние (проекция) ушной раковины от сосцевидного отростка составляет от 10 до 17–20 мм (от сосцевидного отростка до свободного края завитка).
Ушная раковина немного наклонена назад, так что длинная ось создает угол около 8 ° с позадичелюстной (ретромандибулярной) линией. Верхняя часть ушной раковины расположена в вертикальной плоскости на одном уровне с бровью. Нормальное отстояние (проекция) ушной раковины от сосцевидного отростка составляет от 10 до 17–20 мм (от сосцевидного отростка до свободного края завитка).
У детей ушная раковина шире и короче. Отношение высоты к ширине увеличивается с ростом уха, достигая в зрелом возрасте около 7: 4. В зависимости от положения ушной раковины ее поверхность может быть описана как передняя или боковая, а также задняя или медиальная. Спереди завиток должен быть виден на 2–5 мм в поперечном направлении, располагаясь позади противозавитка.
Передняя (боковая) ушная поверхность
Контур или край ушной раковины образован завитком, не полностью свернутой трубкой, который образует желоб или ямку раковины вдоль большей части его длины. Завиток начинается спереди и выходит из полости раковины уха в виде ножки завитка, и в итоге образует закругленную дугу. Часто на завитке имеется выпуклость или бугорок, известный как бугорок Дарвина.
Часто на завитке имеется выпуклость или бугорок, известный как бугорок Дарвина.
Внутри от завитка находится противозавиток, составляющая часть дна ушной раковины и ограничивающая раковину. Сверху у противозавитка имеются две ножки: верхняя и нижняя, между которыми лежит треугольная ямка. Снизу противозавиток присоединяется к противокозелку.
Как завиток, так и противозавиток видны спереди, но противозавиток больше выступает по мере того, как он проходит сверху вниз, создавая угол примерно 20 ° между плоскостями завитка и противозавитка. Нижняя ножка противозавитка ориентирована более высоко у высоких людей с длинными ушами. У детей нижняя ножка противозавитка ориентирована более горизонтально.
Раковина — это неполная полость, которая ведет в слуховой канал. Острый верхний край раковины образован нижней ножкой противозавитка, а нижний край — острыми краями козелка и противокозелка, которые нависают над раковиной. В противоположность этому, боковой край раковины гладкий, свернутый и образованный противозавитком.
Между козелком и противокозелком находится заметная межкозелковая ямка с острыми краями. У пожилых пациентов из этой ямки часто выступает пучок волос.
Долька — единственная часть ушной раковины без хрящевого каркаса. Около трети ее периметра прилегает к щеке, а остальная часть свисает свободно.
Кожа передней поверхности ушной раковины плотно прилегает к нижележащему перихондрию и между ними почти нет жира. Сосуды и нервы лежат в полоске фасции, которая разделяет кожу и перихондрий.
Сальные и потовые железы присутствуют в треугольной ямке и вокруг наружного слухового прохода соответственно.
Кожный покров задней поверхности сильно отличается от плотно связанной, обезжиренной кожи передней поверхности ушной раковины. Задняя поверхность покрыта кожей, которая может сморщиться и скользить по нижележащему хрящу. Это происходит благодаря 2-м слоям жира, поверхностному плотному и рыхлому глубокому. В слое фасции, разделяющей эти слои жировой ткани, проходят нервы, кровеносные и лимфатические сосуды.
Задняя (медиальная) ушная поверхность
Задняя поверхность ушной раковины в основном скрыта от глаз, поскольку ушная раковина выступает всего в 10 мм от сосцевидного отростка. Поверхность характеризуется выступами и бороздками, обратными тем, которые видны на передней поверхности ушной раковины.
Основные возвышения образованы ладьей, раковиной и треугольной ямкой. Треугольная ямка лежит между этими возвышениями.
Ушной хрящ
Ушная раковина приобретает свою форму, внешний вид и гибкость благодаря нижележащей извилистой хрящевой пластинке. Вся ушная раковина, кроме дольки, имеет хрящ в качестве основы.
Уникальная структура ушной раковины, включая выступы и складки в хряще, позволяет сгибать, складывать и сдавливать ее без дискомфорта и последствий. Тонкий, очень плотный слой перихондрия покрывает хрящ ушной раковины.
Передняя / боковая поверхность хряща очень напоминает саму ушную раковину, поскольку она покрыта только тонким слоем кожи.
Завиток изгибается в переднезаднем направлении от ножки завитка, а затем идет назад, образуя хрящевой край ушной раковины. Ладьевидная ямка располагается между завитком и противозавитком.
Противокозелок и козелок разделены межкозелковой ямкой. Раковина и козелок продолжают медиально, образуя хрящевую часть наружного слухового прохода. Эта хрящевая часть входит в костную часть наружного слухового прохода и сливается с ним.
Мышцы ушной раковины
Небольшие внешние мышцы и связки уха обеспечивают прикрепление и поддержку ушной раковины, прочно удерживая ее на костном черепе. Тонус крошечных рудиментарных внутренних мышц обеспечивает структурную поддержку ушной раковины и способствует ее характерной извилистой и складчатой конфигурации
Внешние мышцы состоят из задней, верхней и передней ушной мышц.
Задняя мышца состоит из верхнего и нижнего пучков, поддерживаемых задней ушной связкой. Мышца начинается из надкостницы сосцевидного отростка и прикрепляется к хрящу в области нижней части конхального возвышения. Задняя ушная связка усиливает заднюю ушную мышцу. Эти мышцы иннервируются задней ушной ветвью лицевого нерва и кровоснабжаются задними ушными сосудами.
Задняя ушная связка усиливает заднюю ушную мышцу. Эти мышцы иннервируются задней ушной ветвью лицевого нерва и кровоснабжаются задними ушными сосудами.
Верхняя ушная мышца представляет собой короткую, но сильную мышцу, начинается от надчерепного апоневроза и прикрепляется в возвышение треугольной ямки на задней поверхности ушной раковины. Она покрыта слоями поверхностной височной фасции и получает иннервацию от височной ветви лицевого нерва. Верхняя ушная мышца получает кровоснабжение от небольших ветвей поверхностных височных сосудов.
Передняя ушная мышца обеспечивает дальнейшую поддержку ушной раковины спереди. Она начинается от скуловой дуги и надчерепного апоневроза и прикрепляется в области ножки завитка. Она кровоснабжается ветвями поверхностных височных сосудов и получает иннервацию от ушно-височного нерва и височной ветви лицевого нерва. Передняя ушная мышца поддерживается одноименной связкой.
Собственные мышцы состоят из крошечных смещенных вперед и назад рудиментарных мышц, которые соединяют и перекрывают выпуклости и вогнутости ушной раковины. В передней части вокруг конхи расположены мышцы helicis major, helicis minor, tragicus и antitragicus. Сзади расположены четыре основные внутренние связки, а также вертикально и горизонтально расположенные мышечные волокна, соединяющие и поддерживающие хрящевые извилины ушной раковины.
В передней части вокруг конхи расположены мышцы helicis major, helicis minor, tragicus и antitragicus. Сзади расположены четыре основные внутренние связки, а также вертикально и горизонтально расположенные мышечные волокна, соединяющие и поддерживающие хрящевые извилины ушной раковины.
Иннервация ушной раковины
Ушная раковина получает иннервацию от ветвей большого ушного нерва, малого затылочного нерва, ушно-височного нерва, лицевого нерва и блуждающего нерва.
Большинство из них являются сенсорными, с некоторыми вазомоторными и секреторными волокнами, возникающими из лицевого нерва.
Большой ушной нерв обеспечивает наиболее значительную чувствительную иннервацию ушной раковины. Он возникает из волокон второго и третьего шейных нервов. Нерв у уха делится на переднюю и заднюю ветви. Большой ушной нерв также иннервирует переднюю и верхнюю стенки наружного слухового прохода.
Малый затылочный нерв также возникает из волокон второго, а иногда и третьего, шейных нервов. Интернирует скальп, а также верхнюю часть черепной поверхности ушной раковины.
Интернирует скальп, а также верхнюю часть черепной поверхности ушной раковины.
Ушновисочный нерв — это ветвь заднего ствола нижнечелюстной ветви тройничного нерва. Хотя это в основном сенсорный нерв, он также несет симпатические и парасимпатические волокна и ганглиозные ветви, которые связываются с отическим ганглием. Аурикулотемпоральный нерв проходит преимущественно с поверхностными височными сосудами по скуловой дуге к виску. Сенсорные ветви от аурикулотемпорального нерва иннервируют козелок, нижнюю часть противозавитка, передне-верхнюю часть ладьевидной ямки и завиток и ножку завитка. Он также иннервирует заднюю стенку слухового прохода и барабанную перепонку.
Моторные ветви лицевого нерва иннервируют внешние и внутренние аурикулярные мышцы. Вегетативные симпатические волокна, проходящие с лицевым нервом, обеспечивают вазомоторную и секреторную функцию сосудов и желез ушной раковины.
Кровоснабжение ушной раковины
Наружное кровоснабжение ушная раковина получает через ветви наружной височной артерии спереди и задней ушной артерии сзади.
Угловые раковины эргономичный вариант. Прямоугольные, круглые и полукруглые модели раковин в ванную комнату.
Удобство пользования раковиной во многом зависит от ее формы и конструкции. Например, угловая модель – оптимальный вариант для маленькой ванной комнаты. Какую же раковину выбрать?
На фото:
Форма раковины
На любой вкус. Вы можете выбрать для своей ванной круглую, квадратную, овальную, прямоугольную и даже треугольную раковину. Главное — заранее выбрать место и тип установки.
- Круглые и овальные раковины. Форму усеченной окружности или овала имеет большинство недорогих моделей. Пользоваться ими очень удобно: «срезанной» стороной они примыкают к стене, а остальные остаются свободными. Чаще всего такие раковины невелики по размеру, хотя в продаже можно встретить и крупные экземпляры. Круглую или овальную модель можно подобрать для ванной в любом стиле — как в классическом, так и в современном.

На фото:
Круглые раковины могут быть любого типа — настольные, полупьедесталы, «тюльпаны» и даже встраиваемые модели.
- Квадратные и прямоугольные раковины. Такие модели обычно имеют закругленные углы и круглую или овальную чашу. Реже встречаются изделия в виде правильной геометрической фигуры, с виду напоминающие ящик. Прямоугольные и квадратные раковины, как правило, имеют довольно внушительные размеры. Эти модели больше подходят для ванной комнаты в современном стиле.
На фото:
Форма чаши раковины — это ее внешние очертания. У прямоугольного куба вполне может оказаться «выемка» округлой формы.
- Угловые раковины. Это палочки-выручалочки для маленьких (в том числе гостевых) санузлов. Они преимущественно выглядят как треугольники с закругленным или срезанным основанием. Размеры – компактные, специально для соответствующих помещений.
 Выпускаются также оригинальные угловые модели, у которых чаша развернута боком к стене.
Выпускаются также оригинальные угловые модели, у которых чаша развернута боком к стене.
На фото:
Угловые раковины позволяют рационально организовать пространство небольших санузлов.
Раковины: детали и оборудование
Технологии комфорта. У многих моделей передний бортик вертикально скошен книзу. Это сделано не ради красоты. Так удобнее пользоваться раковиной — к ней можно подойти ближе, то есть не придется тянуть руки, да и брызг будет меньше. Существуют коллекции, рассчитанные на людей с ограниченными возможностями и престарелых. У таких раковин вогнутый передний бортик и широкие боковины, на которые можно опереться.
Из полезных деталей стоит отметить также углубления по краям чаши или за ней, выполняющие функцию мыльниц. В некоторых изделиях есть защитная панель, которая не дает брызгам попадать в щель между раковиной и стеной. Иногда она снабжается отверстиями для монтажа настенного смесителя. В некоторых случаях подвесные умывальники оснащаются полками, которые монтируются по бокам сифона. Очень удобны раковины с крылом или полотенцедержателем. В одних моделях последний имеется «по умолчанию», в других же доступен по желанию заказчика.
В некоторых случаях подвесные умывальники оснащаются полками, которые монтируются по бокам сифона. Очень удобны раковины с крылом или полотенцедержателем. В одних моделях последний имеется «по умолчанию», в других же доступен по желанию заказчика.
На фото:
Брызгозащитный «экран», увеличенные бортики для мыльницы или чаша со столешницей — все эти детали делают умывальник особенно удобным.
На что надо обратить внимание при выборе раковины?
- Тип смесителя. Не все раковины и смесители «совместимы» друг с другом. Поэтому их лучше покупать одновременно. Например, раковина без отверстия подойдет лишь для настенного или настольного смесителя. Для большинства же других моделей необходимы раковины с отверстиями — одним, двумя или тремя.
Что выбирать: раковину под красивый смеситель или смеситель под необычную раковину — вот в чем вопрос.
Модель Tao от фабрики Regia, дизайн Rapisarda Bruna.
- Наличие перелива. Так называется отверстие, через которое сливается вода, если раковина переполняется. Оно есть не у всех изделий. Иногда перелив спрятан под декоративной накладкой, и его можно сразу не заметить.
- Донный клапан. Это устройство, перекрывающее слив воды из раковины. Донный клапан может продаваться вместе со смесителем или в комплекте с раковиной. В первом случае он рассчитан на стандартное сливное отверстие, во втором — имеет размер, подходящий для данной конкретной модели.
На фото:
Донный клапан может быть частью раковины. В этом случае он выполняется в дизайне чаши, украшает ее. А не просто закрывает слив унифицированной «хромированной пробкой».
Выпускаются донные клапаны полуавтоматические и с «ручным» управлением. В одном случае сливное отверстие перекрывается нажатием небольшого рычага на смесителе. В другом — слив можно закрыть, нажав на сам колпачок сливного отверстия. Открывается он так же, что не очень удобно — приходится погружать руку в грязную воду.
Открывается он так же, что не очень удобно — приходится погружать руку в грязную воду.
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Новый треугольный элемент оболочки для композитов с учетом деформации сдвига
Два основных подхода, используемых для разработки общих элементов оболочки: изгиб пластины и наложение мембраны, что оставляет два эффекта несвязанными, по сравнению с формулами, основанными на трехмерной механике сплошной среды, которые могут учитывать такое взаимодействие в учетную запись. Первый способ совмещения изгиба пластины и мембраны очень прост и может быть эффективным для некоторых приложений. По этой причине мы полагаемся здесь на общий подход, основанный на механике сплошной среды, для теории оболочек Нагди-Рейсснера-Миндлина [1], [2], [3], [4], [5], [6], [7] ].
Первый способ совмещения изгиба пластины и мембраны очень прост и может быть эффективным для некоторых приложений. По этой причине мы полагаемся здесь на общий подход, основанный на механике сплошной среды, для теории оболочек Нагди-Рейсснера-Миндлина [1], [2], [3], [4], [5], [6], [7] ].
Конечный элемент, основанный на такой формулировке, может сходиться к точному решению, независимо от геометрии оболочки, и адекватно учитывает эффекты мембраны, изгиба, связанного изгиба мембраны и сдвига.Для моделирования сложных инженерных сооружений часто используются треугольные конечные элементы. Треугольные элементы оболочки также могут более успешно справляться с серьезными трудностями при разработке конечных элементов оболочки, связанными с явлением блокировки для оболочек с преобладанием изгиба [8], [9], [10], [11].
Фиксирующее отверждение для мембран и сдвигов было интересной темой исследований. Было предложено много разных техник. Методы сокращенного и выборочного интегрирования [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22] являются наиболее простое лекарство, которое может успешно уменьшить числовую блокировку. Однако уменьшенная и избирательная интеграция также может привести к дефициту ранга из-за паразитных режимов. Альтернативным лечением блокировки является метод предполагаемых естественных деформаций (ANS) [23], [24], [25], который демонстрирует лучшую точность и надежность. Одна из простейших и эффективных формулировок поперечного сдвига предложена Хьюзом и Тейлором [26] для трехузлового пластинчатого изгибающего элемента. Более усовершенствованный ANS сначала используется для 4-узлового элемента оболочки, называемого MITC4 (смешанная интерполяция тензорных компонентов), который широко используется в инженерной практике [27].
Однако уменьшенная и избирательная интеграция также может привести к дефициту ранга из-за паразитных режимов. Альтернативным лечением блокировки является метод предполагаемых естественных деформаций (ANS) [23], [24], [25], который демонстрирует лучшую точность и надежность. Одна из простейших и эффективных формулировок поперечного сдвига предложена Хьюзом и Тейлором [26] для трехузлового пластинчатого изгибающего элемента. Более усовершенствованный ANS сначала используется для 4-узлового элемента оболочки, называемого MITC4 (смешанная интерполяция тензорных компонентов), который широко используется в инженерной практике [27].
Ли и Бат [28] также предложили трехузловой элемент оболочки MITC3, но этот элемент не свободен от блокировки сдвига. Когда выполняется точное интегрирование, элемент MITC3 блокируется. Если для оценки энергии сдвига используется одна точка, блокировка устраняется, но элемент имеет одну ложную моду. Совсем недавно MITC3 + [29] был разработан как новый трехузловой конечный элемент с треугольной оболочкой (Lee et al. , 2014) для повышения производительности MITC3. Здесь функция кубического пузыря используется для интерполяции вращений, чтобы обогатить поля смещения изгиба.Точно так же был разработан новый элемент оболочки MITC4 + [30], чтобы обеспечить значительно улучшенную производительность в искаженных сетках по сравнению с элементом оболочки MITC4 [27].
, 2014) для повышения производительности MITC3. Здесь функция кубического пузыря используется для интерполяции вращений, чтобы обогатить поля смещения изгиба.Точно так же был разработан новый элемент оболочки MITC4 + [30], чтобы обеспечить значительно улучшенную производительность в искаженных сетках по сравнению с элементом оболочки MITC4 [27].
Наша предыдущая работа по этому вопросу основана на разработке 3-узловых элементов DKT [31] и 4-узловых DKQ [32] для тонких листов с использованием методов дискретного сдвига и предполагаемых естественных деформаций (ANS) для устранения сдвиговых деформаций [ 10]. Элементы DKT и DKQ основаны на модели пластины Рейсснера-Миндлина и накладывают только дискретное ограничение Кирхгофа для устранения эффектов сдвига.Первые попытки включить деформацию сдвига с помощью треугольного элемента, называемого DST (Discrete Shear Triangular) [33], и четырехугольного элемента, называемого DSQ (Discrete Shear Quadrateral) [34]. К сожалению, в проблеме с толстой пластиной ни один из них не проходит тест на исправление. DST-BK был предложен Батозом и Катили [35] для улучшения элемента DST. В рецепте используется метод свободной рецептуры и несовместимые режимы. Элемент DST-BK проходит патч-тесты и дает хорошие результаты при проблемах с тонкими и толстыми пластинами.Еще одно направление в предыдущих работах — пластинчатый элемент PQI с набором несовместимых режимов изгиба, предложенный в [36], [37], [38]. В задачах с тонкими пластинами этот элемент дает такие же характеристики, как и элемент DKQ. Кроме того, элемент PQI также дает отличные характеристики при анализе толстых листов без использования каких-либо регулируемых параметров. Элементы DKMT и DKMQ, основанные на гипотезе Рейсснера-Миндлина [6], [7], также введены Катили [39], [40] для анализа задач о толстых и тонких пластинах. Эти элементы требуют только непрерывности C 0 .Применение элементов DKMQ и DKMT в задачах о пластинах и оболочках представлено в [41], [42], [43], [44], [45], [46], [47], [48], [49]. , [50], [51], [52], [53], [54].
DST-BK был предложен Батозом и Катили [35] для улучшения элемента DST. В рецепте используется метод свободной рецептуры и несовместимые режимы. Элемент DST-BK проходит патч-тесты и дает хорошие результаты при проблемах с тонкими и толстыми пластинами.Еще одно направление в предыдущих работах — пластинчатый элемент PQI с набором несовместимых режимов изгиба, предложенный в [36], [37], [38]. В задачах с тонкими пластинами этот элемент дает такие же характеристики, как и элемент DKQ. Кроме того, элемент PQI также дает отличные характеристики при анализе толстых листов без использования каких-либо регулируемых параметров. Элементы DKMT и DKMQ, основанные на гипотезе Рейсснера-Миндлина [6], [7], также введены Катили [39], [40] для анализа задач о толстых и тонких пластинах. Эти элементы требуют только непрерывности C 0 .Применение элементов DKMQ и DKMT в задачах о пластинах и оболочках представлено в [41], [42], [43], [44], [45], [46], [47], [48], [49]. , [50], [51], [52], [53], [54].
Целью данной статьи является развитие наших предыдущих работ и соответствующее расширение сложных задач. Предлагаемый элемент имеет три узла и шесть степеней свободы на узел и называется элементом DKMT18. Этот новый элемент оболочки учитывает энергию сопряженной изгибной мембраны. Элемент DKMT18 проходит классические патч-тесты в задачах с толстыми и тонкими пластинами и обеспечивает решения, которые быстрее сходятся к эталонным решениям без блокировки сдвига и каких-либо паразитных мод.
Работа организована следующим образом. Кинематическая гипотеза для модели оболочки и выбор систем отсчета объясняются в разделе 2. Формулировка элемента DKMT18 определена в разделе 3 с деталями деформации мембраны, деформаций кривизны и предполагаемого поля деформации сдвига. Матрица жесткости для мембраны, изгиба и сдвига для элемента DKMT18, включая фиктивную жесткость, определена в разделе 4. В разделе 5 мы представляем результаты численного моделирования для различных изотропных и композитных оболочек, включая несколько классических эталонных тестов. Заключительные замечания изложены в разделе 6.
Заключительные замечания изложены в разделе 6.
Три новых треугольных элемента оболочки ANCF, представленные треугольниками Безье
Фарин, Г .: Кривые и поверхности для CAGD: Практическое руководство. Морган Кауфманн, Сан-Матео (2001)
Google Scholar
Эрненс, Д .: Методы конечных элементов с точным геометрическим представлением. Магистерская работа, Делфтский технологический университет (2011 г.)
Пигль, Л., Тиллер, В .: Книга NURBS, 2-е изд. Спрингер, Берлин (1997)
Книга Google Scholar
Роджерс, Д.Ф .: Введение в NURBS: с исторической точки зрения. Морган Кауфманн, Сан-Матео (2001)
Google Scholar
Шабана, А.А .: Вычислительная динамика, 2-е изд. Уайли, Нью-Йорк (2001)
MATH Google Scholar

Шабана А.А. Уникальность геометрического представления в конечно-элементных формулировках с большим вращением. J. Comput. Нелинейный Дин. 5 , 044501 (2010)
Артикул Google Scholar
Коттрелл, Дж. А., Хьюз, Т. Дж. Р., Базилевс, Ю.: Изогеометрический анализ — на пути к интеграции CAD и FEA. Уайли, Нью-Йорк (2009)
Книга Google Scholar
Хьюз Т.Дж.Р., Коттрелл Дж.А., Базилевс Ю.И .: Изогеометрический анализ: САПР, конечные элементы, NURBS, точная геометрия и уточнение сетки. Comput. Методы Прил. Мех. Англ. 194 (39), 4135–4195 (2005)
MATH MathSciNet Статья Google Scholar
Санборн, Г.Г., Шабана, А.А.: Рациональный метод конечных элементов, основанный на формулировке абсолютных узловых координат. Нелинейный Дин. 58 (3), 565–572 (2009)
MATH MathSciNet Статья Google Scholar

Санборн, Г.Г., Шабана, А.А.: Об интеграции автоматизированного проектирования и анализа с использованием формулировки абсолютных узловых координат конечных элементов. Multibody Syst. Дин. 22 (2), 181–197 (2009)
MATH Статья Google Scholar
Шабана, А.А .: Формулировка абсолютных узловых координат для анализа больших вращений и деформаций гибких тел. Технический отчет. № MBS96-1-UIC, Иллинойсский университет в Чикаго (1996)
Шилен, В .: Направления исследований динамики многотельных систем. Multibody Syst. Дин. 18 , 3–13 (2007)
MATH MathSciNet Статья Google Scholar
Шабана А.А .: Обзор динамики многотельных гибких тел в прошлом и в недавнем прошлом. Multibody Syst. Дин. 1 , 189–222 (1997)
MATH MathSciNet Статья Google Scholar

Дмитроченко, О.Н., Погорелов, Д.Ю .: Обобщение пластинчатых конечных элементов для постановки абсолютных узловых координат. Multibody Syst. Дин. 10 (1), 17–43 (2003)
MATH Статья Google Scholar
Дюфва, К., Шабана, А.А .: Анализ структур тонких пластин с использованием формулировки абсолютных узловых координат. Proc. Inst. Мех. Eng., Proc., Часть K, J. Multi-Body Dyn. 219 , 345–355 (2005)
Google Scholar
Тиан, К., Чен, Л., Чжан, Ю.К., Янг, Дж .: Эффективный гибридный метод моделирования динамики многотельных тел, основанный на формулировке абсолютных узловых координат. J. Comput. Нелинейный Дин. 4 , 021009 (2009)
Артикул Google Scholar
Лю, К., Тиан, К., Ху, Х.Ю .: Динамика крупномасштабной жестко-гибкой многотельной системы, состоящей из многослойной композитной пластины. Multibody Syst. Дин. 26 (3), 283–305 (2011)
Multibody Syst. Дин. 26 (3), 283–305 (2011)
MATH MathSciNet Статья Google Scholar
Ян, Д., Лю, К., Тянь, К., Чжан, К., Лю, X.N., Ху, Г.К .: Новый элемент оболочки с изогнутым градиентом и дефицитом абсолютных узловых координат для моделирования тонких структур оболочки. Нелинейный Дин. 74 , 153–164 (2013)
MathSciNet Статья Google Scholar
Лан, П., Шабана, А.А.: Интеграция геометрии B-сплайна и анализа конечных элементов ANCF. Нелинейный Дин. 61 , 193–206 (2010).
MATH MathSciNet Статья Google Scholar
Миккола, А.М., Шабана, А.А., Санчес-Реболло, К., Хименес-Октавио, Дж.Р .: Сравнение поверхностей ANCF и B-сплайнов. Multibody Syst. Дин. 30 (2), 119–138 (2013).
MathSciNet Статья Google Scholar
Фарин, Г .: Треугольные пятна Бернштейна – Безье. Comput. Помощь Geom. Des. 3 (2), 83–127 (1986)
MathSciNet Статья Google Scholar
Ямасита, Х., Сугияма, Х .: Численная сходимость конечно-элементных решений нерациональных B-сплайновых элементов и формулировка абсолютных узловых координат. Нелинейный Дин. 67 (1), 177–189 (2012)
MATH MathSciNet Статья Google Scholar
Шабана А.А., Хамед А.М., Мохамед А.Н.А., Джаякумар П., Летервуд М.Д .: Использование B-сплайна в анализе методом конечных элементов: сравнение с геометрией ANCF.J. Comput. Нелинейный Дин. 7 (1), 011008 (2012)
Артикул Google Scholar
Нада, А.А .: Использование B-сплайновой поверхности для моделирования сплошных пластин с большими деформациями: процедура и приложения. Нелинейный Дин. 72 , 243–263 (2013)
MATH MathSciNet Статья Google Scholar
Баухау, О.А., Хан, С.Л., Миккола, А.М., Матикайнен М.К .: Сравнение абсолютной узловой координаты и геометрически точных формулировок для балок. Multibody Syst. Дин. 32 (1), 67–85 (2013).
MathSciNet Статья Google Scholar
Миккола, А.М., Шабана, А.А.: Без инкрементная процедура конечных элементов для анализа большой деформации пластин и оболочек в приложениях механических систем. Multibody Syst. Дин. 9 (3), 283–309 (2003)
MATH MathSciNet Статья Google Scholar
Матикайнен, М.К., Валкеапяя, А.И., Миккола, А.М., Шваб, А.Л .: Исследование элементов четырехугольной пластины средней толщины на основе формулировки абсолютных узловых координат. Multibody Syst. Дин. (2013). DOI: 10.1007 / s11044-013-9383-6
Google Scholar
Лю, К., Тиан, К., Янь, Д., Ху, Х.Ю .: Динамический анализ мембранных систем, подвергающихся общему движению с большими деформациями и складками через тонкие элементы оболочки из ANCF.Comput. Методы Прил. Мех. Англ. 258 , 81–95 (2013)
MATH MathSciNet Статья Google Scholar
Дмитроченко, О., Миккола, А.М .: Два простых треугольных пластинчатых элемента, основанные на формулировке абсолютных узловых координат. J. Comput. Нелинейный Дин. 3 (4), 041012-1–041012-8 (2008)
Артикул Google Scholar
Шпехт, Б .: Модифицированные функции формы для трехузлового гибочного элемента пластины, прошедшего испытание на исправление. Int. J. Numer. Методы англ. 26 (3), 705–715 (1988)
MATH MathSciNet Статья Google Scholar
Морли, Л.С.Д .: Элемент, изгибающий пластину с постоянным моментом. J. Strain Anal. 6 (1), 20–24 (1971)
Артикул Google Scholar
Мохамед А.А .: Трехмерный полностью параметризованный треугольный пластинчатый элемент, основанный на формулировке абсолютных узловых координат. J. Comput. Нелинейный Дин. 8 (4), 041016-1–041016-7 (2013)
Google Scholar
Убах, П.А., Оньяте, Э .: Новый конечный треугольник оболочки без вращения, точно с использованием геометрических данных. Comput. Методы Прил. Мех. Англ. 199 (5), 383–391 (2010)
MATH Статья Google Scholar
Лю, Ю.: Треугольные поверхности Безье с приблизительной непрерывностью. Университет Ватерлоо, доктор философии. Диссертация (2008)
Ши, Ф .: Компьютерное геометрическое проектирование и неоднородный рациональный B-сплайн. Издательство высшего образования, Пекин (2001) (на китайском языке)
Google Scholar
Манн, С .: Корректировка непрерывности треугольных участков Безье, сохраняющих полиномиальную точность. Отчет об исследовании CS-2000-01 (2000)
Лю Д., Хошек Дж .: Условия непрерывности GC 1 между смежными прямоугольными и треугольными участками поверхности Безье. Comput. Помощь Дес. 21 (4), 194–200 (1989).
MATH Статья Google Scholar
Шабана, А.А., Миккола, А.М .: Использование формулировки абсолютных узловых координат конечных элементов при моделировании разрывов откосов. J. Mech. Des. 125 , 342–350 (2003)
Артикул Google Scholar
Шабана, А.А., Македа, Л.Г .: Разрывы на склоне в формулировке абсолютных узловых координат конечных элементов: элементы с дефицитом градиента. Multibody Syst. Дин. 20 (3), 239–249 (2008)
MATH MathSciNet Статья Google Scholar
Бат, К.Дж .: Процедуры конечных элементов. Прентис-Холл, Нью-Джерси (1996)
Google Scholar
Белычко, Т., Лю, В.К., Моран, Б., Элькходары, К.И .: Нелинейный конечный элемент для сплошных сред и структур. Уайли, Нью-Йорк (2013)
Google Scholar
Герстмайр Дж., Шабана А.А.: Эффективная интеграция упругих сил и тонких трехмерных балочных элементов в формулировке абсолютных узловых координат. В: Материалы тематической конференции Multibody Dynamics Eccomas, Мадрид, Испания, 21–24 июня (2005 г.)
Google Scholar
Лю, К., Тиан, К., Ху, Х.Ю .: Новые пространственные изогнутые балки и цилиндрические оболочечные элементы с абсолютной узловой координатой без градиента. Нелинейный Дин. 70 (3), 1903–1918 (2012)
MathSciNet Статья Google Scholar
Хусейн, Б., Негрут, Д., Шабана, А.А.: Неявное и явное интегрирование в решении абсолютных узловых координатных дифференциальных / алгебраических уравнений. Нелинейный Дин. 54 , 283–296 (2008).
MATH MathSciNet Статья Google Scholar
Шабана, А.А., Хусейн, Б .: Двухпетлевой метод численного интегрирования разреженных матриц для решения дифференциальных / алгебраических уравнений: приложение к многотельным системам. J. Sound Vib. 327 , 557–563 (2009)
Артикул Google Scholar
Хусейн, Б., Шабана, А.А.: Неявное численное интегрирование разреженной матрицы жесткого дифференциального / алгебраического уравнения: реализация. Нелинейный Дин. 65 , 369–382 (2011)
MathSciNet Статья Google Scholar
Чанг, Дж., Халберт, Г .: Алгоритм интегрирования по времени для структурной динамики с улучшенной числовой диссипацией: метод обобщенного альфа. J. Appl. Мех. 60 , 371–375 (1993)
MATH MathSciNet Статья Google Scholar
Арнольд, М., Брюлс, О .: Сходимость обобщенной альфа-схемы для механических систем со связями. Multibody Syst. Дин. 18 , 185–202 (2007).
MATH MathSciNet Статья Google Scholar
Тиан, К., Чжан, Ю., Чен, Л., Янг, Дж. Дж .: Моделирование плоских гибких многотельных систем с зазором и вращающимися шарнирами со смазкой. Нелинейный Дин. 60 , 489–511 (2010)
MATH Статья Google Scholar
Тиан, К., Лю, К., Мачадо, М., Флорес, П .: Новая модель сухих и смазанных цилиндрических соединений с зазором в пространственных гибких многотельных системах. Нелинейный Дин. 64 , 25–67 (2011)
MATH Статья Google Scholar
Лю, К., Тиан, К., Ху, Х.Ю .: Динамика и управление пространственной жестко-гибкой многотельной системой с несколькими цилиндрическими соединениями с зазором. Мех. Мах. Теория 52 , 106–129 (2012)
Артикул Google Scholar
Херманс, М .: Параллельное программирование на Фортране 95 с использованием OpenMP (2002). http://www.openmp.org/presentations/miguel/F95_OpenMPv1_v2.pdf
Куликов Г.М., Плотникова С.В. Нелинейная точная геометрия, 12-узловой твердотельный элемент с тремя поступательными степенями свободы на узел. Int. J. Numer. Методы англ. 88 (13), 1363–1389 (2011)
MATH MathSciNet Статья Google Scholar
Арчинега, Р.А., Редди, Дж. Н .: Тензорная формулировка конечных элементов для геометрически нелинейного анализа оболочечных конструкций. Comput. Методы Прил. Мех. Англ. 196 (4), 1048–1073 (2007)
MATH MathSciNet Статья Google Scholar
Тиан, К., Сун, Ю.Л., Лю, К., Ху, Х.Й., Флорес, П .: Цилиндрические соединения с эластогидродинамической смазкой для жестко-гибкой динамики многотела. Comput. Struct. 114 , 106–120 (2013)
Артикул Google Scholar
Сзе К.Ю., Лю X.H., Ло С.Х .: Популярные тестовые задачи для геометрического нелинейного анализа оболочек. Конечный элемент. Анальный. Des. 40 , 1551–1569 (2004)
Артикул Google Scholar
Разработка и применение высокопроизводительного элемента треугольной оболочки и явного алгоритма в OpenSees для строго нелинейного анализа
Разработка и применение высокопроизводительного элемента треугольной оболочки и явного алгоритма в OpenSees для строго нелинейного анализа
- Xinzheng Lu 1, * , Yuan Tian 2 , Chujin Sun 2 , Shuhao Zhang 2
2 Пекинский научно-исследовательский центр стальных и бетонных композитных конструкций, Университет Цинхуа, Пекин, 100084, Китай.
* Автор для переписки: Xinzheng Lu. Электронное письмо: .
(Эта статья относится к этому Специальному выпуску: Достижения приложений OpenSees в гражданском строительстве)
Абстрактные
Программное обеспечение конечных элементов с открытым исходным кодом OpenSees широко используется в сообществе инженеров, занимающихся сейсмическими исследованиями.Однако элементы оболочки и явный алгоритм в OpenSees все еще требуют дальнейших улучшений. Поэтому в этой работе предлагается и реализован в OpenSees треугольный элемент оболочки, NLDKGT, и явный алгоритм. В частности, на основе обобщенной согласованной теории и обновленной лагранжевой формулировки предлагаемый элемент NLDKGT подходит для задач со сложными граничными условиями и сильной нелинейностью. Точность и надежность элемента NLDKGT проверяются на типичных случаях.Кроме того, за счет применения метода интеграции чехарда разработаны явный алгоритм в OpenSees и модальная модель демпфирования. Наконец, стабильность и эффективность предложенного элемента оболочки и явного алгоритма подтверждаются посредством нелинейного анализа истории высотного здания.
Ключевые слова
Треугольный элемент оболочки, явный алгоритм, OpenSees, сильная нелинейность
Цитируйте эту статью
Лу, X., Тянь, Ю., Сан, К., Чжан, С. (2019). Разработка и применение высокопроизводительного элемента треугольной оболочки и явного алгоритма в OpenSees для строго нелинейного анализа. CMES-Компьютерное моделирование в технике и науках, 120 (3) , 561–582.
Треугольные наночастицы золота изменяют характеристики скорлупы и повышают активность антиоксидантных ферментов у моллюска Ruditapes decussatus
Контекст: Наночастицы могут оказывать неблагоприятное воздействие на окружающую среду, но информация об их взаимодействии с морскими организмами ограничена.
Цель: Нашей целью было изучить влияние треугольных наночастиц золота (НЧ Tr-Au) на моллюска Ruditapes decussatus.
Материалы и методы: Моллюски подвергались воздействию Tr-Au1 = 5 мкг / л и Tr-Au2 = 10 мкг / л в течение 2 и 7 дней. Исследовано влияние на структуру оболочки.Для оценки биохимического статуса использовались супероксиддисмутаза (SOD), каталаза (CAT), глутатионтрансфераза (GST), уровни карбонила белка и содержание малонового диальдегида.
Полученные результаты: Просвечивающая электронная микроскопия (ПЭМ) и электронно-дисперсионный рентгеновский микроанализ (EDX) показали, что наночастицы Tr-Au изменяют структуру и морфологию оболочки. Размер НЧ Tr-Au увеличился, образуя частицы агрегата.НЧ Tr-Au увеличивают активность SOD, CAT и GST в жабрах и пищеварительных железах в зависимости от концентрации и времени, что указывает на защиту от окислительного стресса. Повышенное перекисное окисление липидов и уровни карбонила белка подтвердили окислительный стресс.
Заключение: НЧ Tr-Au вызывают окислительный стресс и влияют на структуру раковины моллюсков. Эти результаты могут иметь отношение к другим морским видам.
Ключевые слова: Окислительный стресс; биомаркеры; биомониторинг; двустворчатый.
(Золотая треугольная нанопластина) @ (серебряная оболочка) наноструктуры как высокочувствительные и селективные плазмонные нанозонды для обнаружения сероводорода
Сероводород играет важную роль в жизни живых существ, а его аномальная концентрация связана со многими заболеваниями.Кроме того, газ H 2 S вреден для человека и окружающей среды. Таким образом, обнаружение H 2 S привлекло большое внимание в последние несколько десятилетий. Здесь сообщается о высокочувствительных и селективных плазмонных нанозондах H 2 S (золотое треугольное ядро нанопластинки) @ (серебряная оболочка) (AuTNP @ Ag). Благодаря высокой чувствительности ТНП Au к окружающей среде и легкой сульфуризации серебра ионами серы AuTNP @ Ag проявляет большую чувствительность как к ионам серы, так и к газу H 2 S.Сдвиги плазмонного пика достигают 16 нм для вентиляции 1 ppm сероводорода. Нанозонды AuTNP @ Ag также демонстрируют очень хорошую линейность чувствительности при низких концентрациях ионов серы. Кроме того, достигается превосходная селективность обнаружения ионов серы. С помощью нанозондов AuTNP @ Ag разработан тестовый гель, который может производить видимое невооруженным глазом изменение цвета при воздействии газообразного сероводорода 1–100 ppm. Благодаря высокой чувствительности, линейности и селективности нанозондов Au TNP @ Ag для определения сероводорода эта работа открывает путь для плазмонного обнаружения сероводорода как в биологических, так и в экологических приложениях.
У вас есть доступ к этой статье
Подождите, пока мы загрузим ваш контент… Что-то пошло не так. Попробуй еще раз?| недействительным SetNodes (станд :: shared_ptr | |
| Укажите узлы этого элемента.Подробнее … | |
| virtual int | GetNnodes () override |
| Получить количество узлов, используемых этим элементом, не считая узлов, отмеченных «nullptr» напр. если на границе. | |
| virtual int | GetNdofs () override |
| Получить количество координат в поле, используемое ссылочными узлами. | |
| virtual int | GetNodeNdofs (int n) override |
| Получить количество координат от n-го узла, используемого этим элементом. | |
| virtual std :: shared_ptr | GetNodeN (int n) override |
| Доступ к n-му узлу этого элемента, не считая узлов, отмеченных «nullptr», например. если на границе. | |
| std :: shared_ptr | GetNodeTriangleN (int n) const |
| Получить дескриптор узла n этого элемента среди трех частей треугольника, n = 0..2. | |
| std :: shared_ptr | GetNodeNeighbourN (int n) const |
| Получить дескриптор узла n из трех соседних треугольников, n = 0..2. Даже если nullptr. | |
| void | SetAsNeutral () |
| Устанавливает нейтральное вращение узлов сразу, предполагая, что текущее положение элемента соответствует нулевой деформации. | |
| void | AddLayer (двойная толщина, двойная тета, материал std :: shared_ptr |
| Добавить слой. Подробнее … | |
| void | SetLayerZreferenceCentered () |
| Задайте базовый уровень z элемента оболочки как центрированный по всей толщине. Подробнее … | |
| void | SetLayerZreference (double z_from_bottom) |
| Наложите опорный уровень z элемента оболочки относительно нижней грани нижнего слоя. Примечание! Используйте после того, как вы добавили все слои. | |
| size_t | GetNumLayers () const |
| Получить количество слоев. | |
| const Layer & | GetLayer (size_t i) const |
| Получить дескриптор указанного слоя. | |
| double | GetThickness () |
| Получите общую толщину элемента оболочки (может быть суммой нескольких толщин слоев) | |
| void | ShapeFunctions (ShapeVector & N, const double u, const double v) |
| Заполняет матрицу функции формы N, вычисленную в «естественных» координатах треугольника U и V. | |
| void | ShapeFunctionsDerivativeU (ShapeVector & Nu, const double u, const double v) |
| Заполняет производную матрицу функции формы Nu по отношению к U. Обратите внимание: может удалить u, v parms, вызывающие константу. | |
| void | ShapeFunctionsDerivativeV (ShapeVector & Nv, const double u, const double v) |
| Заполняет матрицу производной функции формы Nv относительно V.Обратите внимание: можно удалить параметры u, v, вызывающие константу. | |
| void | ShapeFunctionsDerivativeX (ShapeVector & Nx, const ChMatrixNM |
| void | ShapeFunctionsDerivativeY (ShapeVector & Ny, const ChMatrixNM |
| 905 заполнит форму матрица производных функции по направлению локального элемента Y.Подробнее … | |
| virtual void | GetStateBlock (ChVectorDynamic <> & mD) override |
| Заполните вектор D текущими значениями поля в правильном порядке элементов. Подробнее … | |
| виртуальная пустота | ComputeKRMmatricesGlobal (ChMatrixRef H, двойной Kfactor, double Rfactor = 0, double Mfactor = 0) переопределить |
| 905 жесткость матрицы Устанавливает | матрицу жесткости масштабируется Kfactor.Подробнее … |
| virtual void | ComputeInternalForces (ChVectorDynamic <> & Fi) override |
| Вычисляет внутренние силы. Подробнее … | |
| void | ComputeInternalForces_impl (ChVectorDynamic <> & Fi, ChState & state_x, ChStateDelta & state_w, bool used_for_differentiation = false) |
| Update () override | |
| Обновить состояние этого элемента. | |
| виртуальная пустота | EvaluateSectionDisplacement (const double u, const double v, ChVector <> & u_displ, ChVector <> & u_rotaz) переопределить |
| virtual void | EvaluateSectionFrame (const double u, const double v, ChVector <> & point, ChQuaternion <> & rot) переопределить |
| 90yz абсолютное положение. точку на оболочке и абсолютное вращение ссылки сечения в параметрических координатах «u» и «v».Подробнее … | |
| virtual void | EvaluateSectionPoint (const double u, const double v, ChVector <> & point) override |
| Получает абсолютное положение xyz точки на оболочке , в параметрических координатах u и v. Подробнее … | |
| virtual void | EvaluateSectionVelNorm (double U, double V, ChVector <> & Result) переопределить |
| Виртуальный метод построения распределения поля скорости.Подробнее … | |
| virtual bool | IsTriangleShell () override |
| Вернуть false, если четырехугольная оболочка — следовательно, параметрические координаты u, v приняты в -1 .. + 1, вернуть true, если треугольная оболочка — следовательно, u, v — предполагаемые естественные координаты треугольника в 0 .. + 1. | |
| void | ComputeInternalJacobians (double Kfactor, double Rfactor) |
| Вычислите якобианы внутренних сил.Подробнее … | |
| virtual int | LoadableGet_ndof_x () override |
| Получает количество степеней свободы, затронутых этим элементом (часть позиции). | |
| virtual int | LoadableGet_ndof_w () override |
| Получает количество степеней свободы, на которые влияет этот элемент (часть скорости). | |
| virtual void | LoadableGetStateBlock_x (int block_offset, ChState & mD) override |
| Получает все DOF, упакованные в один вектор (позиционная часть). | |
| virtual void | LoadableGetStateBlock_w (int block_offset, ChStateDelta & mD) override |
| Получает все степени свободы, упакованные в один вектор (часть скорости). | |
| virtual void | LoadableStateIncrement (const unsigned int off_x, ChState & x_new, const ChState & x, const unsigned int off_v, const ChStateDelta & Dv) override |
| Увеличивает все DOF с использованием дельты. | |
| virtual int | Get_field_ncoords () override |
| Число координат в интерполированном поле, ex = 3 для тетраэдрического конечного элемента или кабеля, = 1 для тепловой задачи и т. д. | |
| virtual int | GetSubBlocks () override |
| Сообщает количество блоков степеней свободы (например, = 1 для тела, = 4 для тетраэдра и т. д.)) | |
| virtual unsigned int | GetSubBlockOffset (int nblock) override |
| Получить смещение i-го подблока степеней свободы в глобальном векторе. | |
| virtual unsigned int | GetSubBlockSize (int nblock) override |
| Получить размер i-го подблока степеней свободы в глобальном векторе. | |
| virtual void | LoadableGetVariables (std :: vector |
| Получить указатели на содержащиеся ChVariables, добавленные к вектору mvars. | |
| виртуальная пустота | ComputeNF (const double U, const double V, ChVectorDynamic <> & Qi, double & detJ, const ChVectorDynamic <> & F, ChVectorDynamic <> * state_Dynamic *, ChVectorDynamic <> * state_Dynamic *, ChVectorDynamic <> * state_Dynamic *) |
| Вычислить N ‘* F, где N — некоторый тип функции формы, вычисляемый в координатах U, V поверхности, каждый в диапазоне -1 .. + 1 F — нагрузка, N’ * F — результирующая обобщенная нагрузка. Также возвращается det [J] с J = [dx / du ,..], что может быть полезно в квадратуре Гаусса. Подробнее … | |
| virtual void | ComputeNF (const double U, const double V, const double W, ChVectorDynamic <> & Qi, double & detJ, const ChVectorDynamic <> & F, ChVectorDynamic <> * , ChVectorDynamic <> * state_w) override |
| Вычислить N ‘* F, где N — некоторый тип функции формы, вычисляемой в координатах U, V, W объема, каждая в диапазоне -1.. + 1 F — нагрузка, N ‘* F — результирующая обобщенная нагрузка. Возвращает также det [J] с J = [dx / du, ..], что может быть полезно в квадратуре Гаусса. Подробнее … | |
| virtual double | GetDensity () override |
| Это необходимо для того, чтобы ChLoaderVolumeGravity мог получить к нему доступ. Подробнее … | |
| virtual ChVector | Переопределение ComputeNormal (const double U, const double V) переопределение |
| Получает нормаль к поверхности в параметрических координатах U, V.Подробнее … | |
| virtual bool | IsTriangleIntegrationNeeded () override |
| Если true, использовать квадратуру по u, v в диапазоне [0..1] как координаты площади треугольника (с z = 1-uv) в противном случае использовать квадратуру по умолчанию над u, v в [-1 .. + 1] как прямоугольные изопараметрические координаты. | |
| virtual bool | IsTrianglePrismIntegrationNeeded () переопределить |
| Если true, использовать квадратурную зависимость от u, v в [0..1] как естественные координаты треугольника (с z = 1-uv) и использовать линейную квадратуру по w в [-1 .. + 1], в противном случае используйте квадратуру по умолчанию для u, v, w в [-1 .. + 1] в виде прямоугольных изопараметрических координат. | |
| ChKblockGeneric & | Kstiffness () |
| Доступ к прокси для жесткости для разреженного решателя. | |
| virtual void | EleIntLoadResidual_F (ChVectorDynamic <> & R, const double c) override |
| (Это стандартное (немного неоптимальное) ведение бухгалтерского учета, так что в дочерних классах вы можете избежать реализации этой функции EleIntLoadResidual_F, если вам не нужна функция EleIntLoadResidual_F более быстрый код) | |
| virtual void | EleIntLoadResidual_Mv (ChVectorDynamic <> & R, const ChVectorDynamic <> & w, const double c) override |
| (Это значение по умолчанию (ОЧЕНЬ НЕОПТИМАЛЬНОЕ) ведение бухгалтерии, так что в этих дочерних классах вы можете избежать функция, если вам не нужен более быстрый код.) | |
| virtual void | EleIntLoadResidual_F_gravity (ChVectorDynamic <> & R, const ChVector <> & G_acc, const double c) переопределить |
| VAL по умолчанию (This book is a book что в детских классах вы можете избежать реализации этой функции EleIntLoadResidual_F_gravity, если вам не нужен более быстрый код. Подробнее … | |
| virtual void | ComputeGravityForces (ChVectorDynamic <> & Fg, const ChVector <> & G_acc) override |
| (Это реализация по умолчанию (ПОТЕНЦИАЛЬНО НЕЭФФЕКТИВНАЯ), так что в дочерних классах вы можете избежать реализации этой функции CompcesGra вам нужен более быстрый код.Эта резервная реализация использует временную ChLoaderGravity, которая применяет нагрузку к элементам, только если они унаследованы ChLoadableUVW, поэтому он может использовать GetDensity () и квадратуру Гаусса. | |
| virtual void | ComputeMmatrixGlobal (ChMatrixRef M) override |
| Возвращает глобальную матрицу масс. Подробнее … | |
| virtual void | InjectKRMmatrices (ChSystemDescriptor & mdescriptor) override |
| Сообщите системному дескриптору, что в этом объекте есть элемент (ы) типа ChKblock (для дальнейшей передачи его в решатель) | |
| virtual void | KRMmatricesLoad (double Kfactor, double Rfactor, double Mfactor) override |
| Добавляет текущие матрицы жесткости K и демпфирования R и массы M в инкапсулированных элементах ChKblock, если они есть.Подробнее … | |
| virtual void | VariablesFbLoadInternalForces (двойной коэффициент = 1.) override |
| Добавляет внутренние силы, выраженные как узловые силы, в инкапсулированные ChVariables в части ‘fb’: qf + = force * factor (Это бухгалтерия по умолчанию (немного неоптимальная), так что в дочерних классах вы можете избежать реализации этой функции VariablesFbLoadInternalForces, если вам не нужен более быстрый код) Добавляет M * q (внутренние массы, умноженные на текущий qb) к Fb, например.Подробнее … | |
| virtual void | ComputeNodalMass () |
| Вычислить узловые массы элемента. | |
| virtual void | EleDoIntegration () |
| Это дополнительно реализуется, если есть какое-то внутреннее состояние, требующее интеграции. | |
| virtual bool | IsTetrahedronIntegrationNeeded () |
| Если это правда, использовать квадратурную зависимость по u, v, w в [0. | |
 Покупайте у самых известных и ведущих продавцов и поднимите полезность мойки на новый уровень.
Покупайте у самых известных и ведущих продавцов и поднимите полезность мойки на новый уровень.  Вы можете выбрать вариант с краном или без него, в зависимости от того, что вам больше подходит.
Вы можете выбрать вариант с краном или без него, в зависимости от того, что вам больше подходит. 


 Керамика очищается раз в 7 дней с помощью кислотосодержащих или простых средств. Изделия из натурального камня очищаются специальными средствами, мягкими губками, салфетками. Пастообразными, гелевыми чистящими составами. Очищаются искусственные покрытия и приводятся до блеска.
Керамика очищается раз в 7 дней с помощью кислотосодержащих или простых средств. Изделия из натурального камня очищаются специальными средствами, мягкими губками, салфетками. Пастообразными, гелевыми чистящими составами. Очищаются искусственные покрытия и приводятся до блеска. Так, круглые раковины – это вечная классика, которая будет уместна в интерьере любой стилистической направленности. Они идеально впишутся как в классический интерьер, так и в более современный.
Так, круглые раковины – это вечная классика, которая будет уместна в интерьере любой стилистической направленности. Они идеально впишутся как в классический интерьер, так и в более современный. Стандартная раковина «на ножке», основным достоинством которой можно считать не только функциональность, но и эстетику. Что ж, действительно, самое достойное решение для габаритной ванной в классическом стиле.
Стандартная раковина «на ножке», основным достоинством которой можно считать не только функциональность, но и эстетику. Что ж, действительно, самое достойное решение для габаритной ванной в классическом стиле. Для их установки потребуется приобретение специального шкафчика, так называемого мойдодыра, в который встроено зеркало. К слову, шкафчик можно использовать не только для хранения бытовых мелочей, но и для того, чтобы скрыть все неприглядные коммуникации.
Для их установки потребуется приобретение специального шкафчика, так называемого мойдодыра, в который встроено зеркало. К слову, шкафчик можно использовать не только для хранения бытовых мелочей, но и для того, чтобы скрыть все неприглядные коммуникации. Его поверхность недостаточно гладкая и слишком пористая, ввиду чего материал сильно подвержен окрашиваю и страдает от малейших механических повреждений.
Его поверхность недостаточно гладкая и слишком пористая, ввиду чего материал сильно подвержен окрашиваю и страдает от малейших механических повреждений.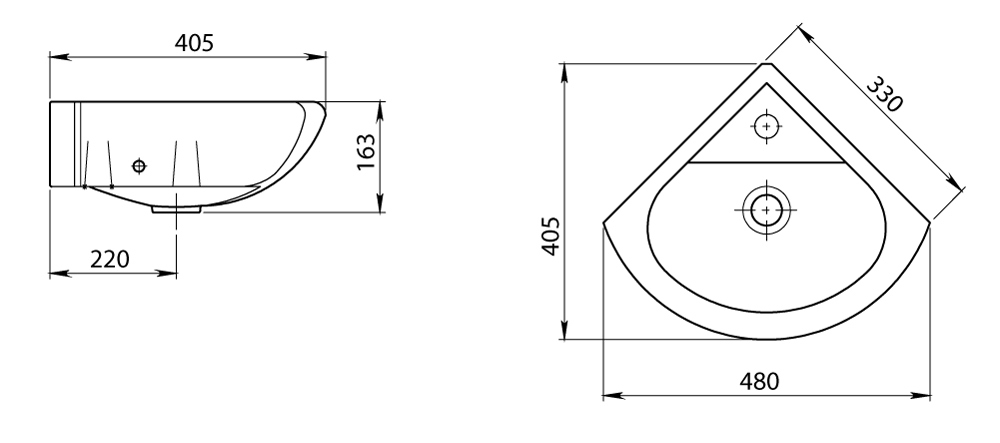
 Выпускаются также оригинальные угловые модели, у которых чаша развернута боком к стене.
Выпускаются также оригинальные угловые модели, у которых чаша развернута боком к стене.