калькулятор расчета и таблица кубатуры пиломатериала 4 и 6 метров
Главная › Новости
Опубликовано: 31.10.2018
Любые строительные работы с применением пиломатериала рано или поздно поставят перед вами вопрос – сколько досок определенного типоразмера будет содержать один куб. Облегчить задачу расчета, привести готовые таблицы-кубатурники, а также рассказать о существующих нюансах перевода кубометров в количество досок и наоборот мы и постараемся в данной статье.
Порядок и методика расчета
Чтобы рассчитать, сколько досок будет в одном кубе, достаточно освежить в памяти знания из курса математики средней школы. Переходим к порядку расчета.
Исходные данные
В расчетах будем отталкиваться от размеров доски. Используется три значения: высота (толщина), ширина и длина. В обозначении сортамента они приводятся в таком же порядке, например 25×150×6000 и указываются в миллиметрах.
Важно! Перед началом расчета не забудьте перевести значения геометрических размеров в метры. Так как мы рассматриваем расчет для нахождения количества досок в 1 метре кубическом, значит и все исходные данные должны быть приведены к размеру в метрах.
Высота и ширина (сечение) обрезного пиломатериала регламентируются ГОСТ 24454-80 «Пиломатериалы хвойных пород. Размеры», хотя у продавцов они могут иметь и другие значения.
Отметим, что для расчетов пиломатериалов специального назначения, отличающихся от стандартной прямоугольной формы в поперечном сечении (к примеру, шпунтованной половой доски), значения размеров высоты и ширины следует принимать по лицевой, «рабочей» ширине поверхности.
Для длины обрезного пиломатериалы наиболее популярные на рынке предложения – это 4-х и 6-ти метровые доски.
Важно! Покупая необрезную доску неизвестных геометрических параметров, размеры её сечения для последующего расчета кубатуры лучше находить как среднее значение между высотой и шириной, измеренных с обеих сторон.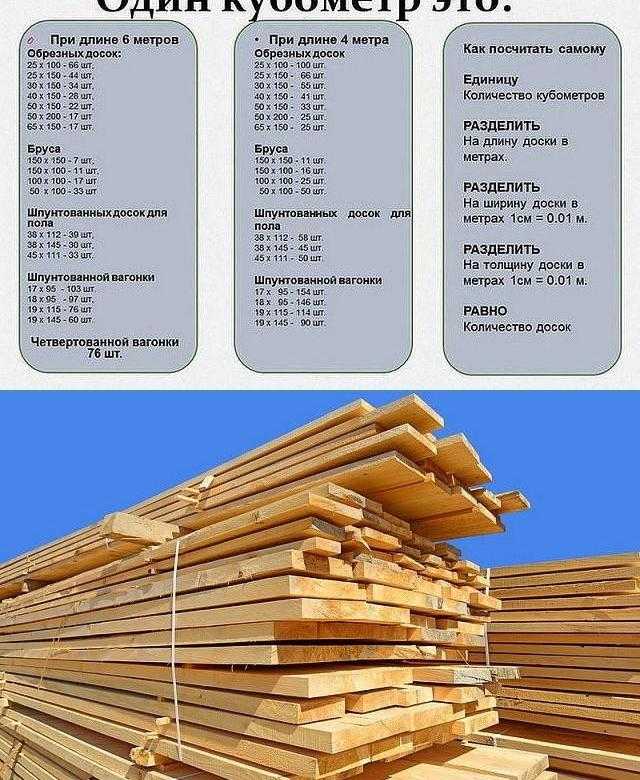
Расчет количества досок в кубе
Отталкиваться будем от простой геометрической формулы: объем равен произведению длин трех сторон. По ней, используя исходные данные, рассчитываем объем одной доски. Затем делим 1 на полученное значение и получаем итоговую цифру сколько досок содержится в кубе в штуках.
Символьной формулой расчет кубатуры доски можно записать так:
1 / (L*h*b) = N, где
h, b, L – высота, ширина и длина доски соответственно, м;
N – количество досок в 1 м3, штук.
Нужно понимать, что расчет по обозначенной формуле носит ориентировочный характер. Число может получиться и дробное, хотя при покупке вы заберете количество, кратное целому и округленное в меньшую сторону. Также производителем пиломатериала могут четко не соблюдаться номинальные значения геометрических размеров, и фактическое количество досок в одном кубе может составить как большее значение, так и меньшее от расчетного. Кроме того, не следует руководствоваться расчетом «впритык».
Не весь купленный пиломатериал может оказаться пригодным к использованию, поэтому процентов 10-15 запаса по количеству, особенно при больших партиях закупки, следует закладывать на брак.
Важно! При покупке объема пиломатериала, превышающего 1 м3, требуйте расчета количества отпускаемой вам доски от всего объема по вышеприведенной формуле (подставляя вместо единицы в числителе нужный вам объем), а не по одному кубу с последующим округлением и умножением – недобросовестные продавцы на этом могут сэкономить.
Расчет покрытия в м2 одним кубометром доски
Данный расчет – частный случай, востребованный когда нужно знать, сколько квадратных метров способен покрыть один метр кубический пиломатериала, например, для половой доски или же стеновой вагонки.
Формула все также проста – нужно полученное по результатам прошлого расчета количество досок в кубе (округленное до целого числа) умножить на площадь одной доски (произведение длины на ширину). Выражаясь символьным языком, это выглядит следующим образом:
S = N * b * L, где
S – площадь в м2, «зашиваемая» 1 м3 доски.
Важно! Расчетное значение площади доски в одном кубометре также получается ориентировочной цифрой, которую, при закупке пиломатериала на необходимый метраж в «квадратах», следует брать с определенным запасом.
Калькуляторы кубатуры досок
Рассмотрев вышеприведенные формулы, в теории становится понятно, как посчитать кубатуру доски. Для повседневного использования и упрощения рутинного процесса на нашем сайте размещены калькуляторы, осуществляющие онлайн-расчет по различным критериям.
Калькулятор расчета количества досок в кубе
Данный калькулятор осуществляет расчет количества досок в штуках, содержащихся в заданном объеме пиломатериала в кубометрах. Чтобы рассчитать искомый показатель, необходимо ввести в соответствующие поля параметры одной доски (ширина, толщина, длина – в мм) и общий объем досок в м3.
Итоговый результат в штуках может иметь дробное значение, но продавцы пиломатериала, как правило, округляют расчетное количество досок в кубе до ближайшего меньшего целого числа, что также учитывает и наш онлайн-калькулятор.
Калькулятор расчета кубатуры досок по их количеству
Нижеприведенный калькулятор будет полезен, когда возникает задача перевести доски в кубы. В качестве исходных данных, как и для предыдущего онлайн-расчета, используется геометрические размеры одной доски в мм и общее количество досок в штуках, для которых нужно определить их кубатуру в м3.
Готовые таблицы количества досок в кубе
Несмотря на простоту формулы определения кубатуры пиломатериала и наличие доступных онлайн-калькуляторов, рассчитывать каждый раз сколько досок в кубе для разных размеров достаточно неудобно. Для избавления от этого рутинного процесса созданы уже готовые таблицы-кубатурники, которыми достаточно удобно пользоваться для быстрого определения количества штук пиломатериала в 1 м3.
Сколько 6-ти метровых досок в 1 кубе: таблица
| Доска-«двадцатка» (толщина 20 мм) | ||
| 20×100×6000 | 83 шт.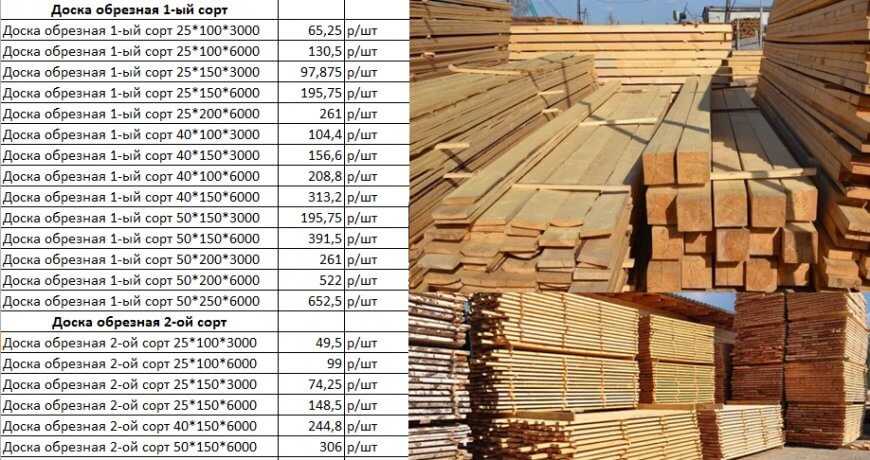 | 49,8 м2 |
| 20×120×6000 | 69 шт. | 49,7 м2 |
| 20×150×6000 | 55 шт. | 49,5 м2 |
| 20×180×6000 | 46 шт. | 49,7 м2 |
| 20×200×6000 | 41 шт. | 49,2 м2 |
| 20×250×6000 | 33 шт. | 49,5 м2 |
| Доска-«двадцатьпятка» (толщина 25 мм) | ||
| 25×100×6000 | 66 шт. | 39,6 м2 |
| 25×120×6000 | 55 шт. | 39,6 м2 |
| 25×150×6000 | 44 шт. | 39,6 м2 |
| 25×180×6000 | 37 шт. | 40 м2 |
| 25×200×6000 | 33 шт. | 39,6 м2 |
| 25×250×6000 | 26 шт. | 39 м2 |
| Доска-«тридцатка» (толщина 30 мм) | ||
| 30×100×6000 | 55 шт. | 33 м2 |
| 30×120×6000 | 46 шт. | 33,1 м2 |
| 30×150×6000 | 37 шт. | 33,3 м2 |
| 30×180×6000 | 30 шт. | 32,4 м2 |
| 30×200×6000 | 27 шт. | 32,4 м2 |
| 30×250×6000 | 22 шт. | 33 м2 |
| Доска-«тридцатидвушка» (толщина 32 мм) | ||
| 32×100×6000 | 52 шт. | 31,2 м2 |
| 32×120×6000 | 43 шт. | 31 м2 |
| 32×150×6000 | 34 шт. | 30,6 м2 |
| 32×180×6000 | 28 шт. | 30,2 м2 |
| 26 шт. | 31,2 м2 | |
| 32×250×6000 | 20 шт. | 30 м2 |
| Доска-«сороковка» (толщина 40 мм) | ||
| 40×100×6000 | 41 шт. | 24,6 м2 |
| 40×120×6000 | 34 шт. | 24,5 м2 |
| 40×150×6000 | 27 шт. | 24,3 м2 |
| 40×180×6000 | 23 шт. | 24,8 м2 |
| 40×200×6000 | 20 шт. | 24 м2 |
| 40×250×6000 | 16 шт. | 24 м2 |
| Доска-«пятидесятка» (толщина 50 мм) | ||
| 50×100×6000 | 33 шт. | 19,8 м2 |
| 50×120×6000 | 27 шт. | 19,4 м2 |
| 50×150×6000 | 22 шт. | 19,8 м2 |
| 50×180×6000 | 18 шт. | 19,4 м2 |
| 50×200×6000 | 16 шт. | 19,2 м2 |
| 50×250×6000 | 13 шт. | 19,5 м2 |
Сколько 4-х метровых досок в 1 кубе: таблица
| Доска-«двадцатка» (толщина 20 мм) | ||
| 20×100×4000 | 125 шт. | 50 м2 |
| 20×120×4000 | 104 шт. | 49,9 м2 |
| 20×150×4000 | 83 шт. | 49,8 м2 |
| 20×180×4000 | 69 шт. | 49,7 м2 |
| 20×200×4000 | 62 шт. | 49,6 м2 |
| 20×250×4000 | 50 шт. | 50 м2 |
| Доска-«двадцатьпятка» (толщина 25 мм) | ||
| 25×100×4000 | 100 шт. | 40 м2 |
| 25×120×4000 | 83 шт. | 39,8 м2 |
| 25×150×4000 | 66 шт. | 39,6 м2 |
| 25×180×4000 | 55 шт. | 39,6 м2 |
| 25×200×4000 | 50 шт. | 40 м2 |
| 25×250×4000 | 40 шт. | 40 м2 |
| Доска-«тридцатка» (толщина 30 мм) | ||
| 30×100×4000 | 83 шт. | 33,2 м2 |
| 30×120×4000 | 69 шт. | 33,1 м2 |
| 30×150×4000 | 55 шт. | 33 м2 |
| 30×180×4000 | 46 шт. | 33,1 м2 |
| 30×200×4000 | 41 шт. | 32,8 м2 |
| 30×250×4000 | 33 шт. | 33 м2 |
| Доска-«тридцатидвушка» (толщина 32 мм) | ||
| 32×100×4000 | 78 шт. | 31,2 м2 |
| 32×120×4000 | 65 шт. | 31,2 м2 |
| 32×150×4000 | 52 шт. | 31,2 м2 |
| 32×180×4000 | 43 шт. | 31 м2 |
| 32×200×4000 | 39 шт. | 31,2 м2 |
| 32×250×4000 | 31 шт. | 31 м2 |
| Доска-«сороковка» (толщина 40 мм) | ||
| 40×100×4000 | 62 шт. | 24,8 м2 |
| 40×120×4000 | 52 шт. | 25 м2 |
| 40×150×4000 | 41 шт. | 24,6 м2 |
| 40×180×4000 | 34 шт. | 24,5 м2 |
| 40×200×4000 | 31 шт. | 24,8 м2 |
| 40×250×4000 | 25 шт. | 25 м2 |
| Доска-«пятидесятка» (толщина 50 мм) | ||
| 50×100×4000 | 50 шт. | 20 м2 |
| 50×120×4000 | 41 шт. | 19,7 м2 |
| 50×150×4000 | 33 шт. | 19,8 м2 |
| 50×180×4000 | 27 шт. | 19,4 м2 |
| 50×200×4000 | 25 шт. | 20 м2 |
| 50×250×4000 | 20 шт. | 20 м2 |
Таблица кубатуры необрезного пиломатериала
Составление готовой точной таблицы для такого рода изделий, как и точный расчет, затруднительны.
Необрезной пиломатериал получают продольным распиливанием бревна на доски без дальнейшей их обработки по кромкам. В такой ситуации в зависимости от участка выпилки меняется и ширина полученной доски, постоянными остаются только длина и высота (толщина).
Чтобы хотя бы примерно представлять, сколько необрезной доски будет в одном кубе, мы приводим типовой вариант таблицы-кубатурника необрезного пиломатериала длиной 6 метров и стандартного ряда толщин 25, 40 и 50 мм:
Особенности практического применения расчета и таблиц
Следует понимать, что алгоритм расчета количества доски в кубе будет одинаков для пиломатериала с различными степенями осушки или же из различных пород древесины. Каких-то дополнительных ухищрений тут не требуется.
Также отметим, что табличные значения являются, хоть и с высокой степень точности, но все-таки ориентировочными данными. В действительности, при подсчете реального количества досок в кубе, многое будет зависеть от плотности укладки штабеля, ведь пиломатериал не прилегает друг к другу идеально плотно, как то подразумевает математическая модель расчета.
Помните об этом, рассчитывайте по формулам или таблицам сколько кубов пиломатериала вам необходимо и рассматривайте приобретение расчетного количества с определенным запасом.
1.2 Комбинации и перестановки
Сначала обратимся к , считая . Хотя это звучит просто, возможно, слишком
просто учиться, это не так. Когда мы говорим о счете, это стенография
для определения размера множества или, чаще, размеров многих
наборы, все с чем-то общим, но разные размеры в зависимости от
один или несколько параметров. Например: сколько исходов возможно
когда бросают кубик? Две кости? $n$ кости? Как сказано, это
двусмысленно: что мы подразумеваем под «результатом»? Предположим, мы бросаем две кости,
скажем, красный кубик и зеленый кубик. Является ли «красный два, зеленый три» другим
результат, чем «красное три, зеленое два»? Если да, мы подсчитываем
количество возможных «физических» исходов, а именно 36. Если нет, то есть
21. Нас даже могут интересовать просто возможные итоги, т.е.
Даже довольно простая первая интерпретация опирается на некоторую степень знание счета; мы сначала выясним два простых факта. В с точки зрения размеров множества, предположим, что мы знаем, что множество $A$ имеет размер $m$ и множество $B$ имеет размер $n$. Каков размер $A$ и $B$ вместе, то есть размер $A\cup B$? Если мы знаем, что $A$ и $B$ не имеют элементов в общий, то размер $A\cup B$ равен $m+n$; если у них есть элементы в общее, нам нужно больше информации. Простая, но типичная проблема этого тип: если мы бросим два кубика, сколько существует способов получить либо 7, либо 11? Так как есть 6 способов получить 7 и два способа получить 11, ответ: $6+2=8$. Хотя этот принцип прост, его легко забыть требование непересекаемости двух множеств и, следовательно, использовать это когда обстоятельства иные. Этот принцип часто называется 9п м_i$. Этот может быть доказано простым рассуждением по индукции.
Почему мы знаем, не перечисляя их всех, что существует 36 исходов?
когда бросают две игральные кости? Мы можем рассматривать результаты как два отдельных
результаты, то есть результат броска кубика номер один и
результат броска кубика номер два.
По каждому из 6 исходов
первый кубик второй кубик может иметь любой из 6 исходов, поэтому сумма равна
$6+6+6+6+6+6=36$ или, более компактно, $6\cdot6=36$. Обратите внимание, что мы
здесь действительно используется принцип сложения: set $A_1$ — это все пары
$(1,x)$, набор $A_2$ — это все пары $(2,x)$ и т. д. это несколько
более тонким, чем кажется на первый взгляд. В этом простом примере
результаты кубика номер два не имеют ничего общего с результатами кубика
номер один. Вот немного более сложный пример: сколько способов
можно ли бросить два кубика так, чтобы два кубика не совпали? То есть,
исключаем 1-1, 2-2 и так далее. Здесь для каждого возможного значения на кубике
число один, есть пять возможных значений кубика номер два, но
это разные пять значений для каждого значения на номере кубика
один. Тем не менее, поскольку все одинаковы, результат равен 5+5+5+5+5+5=30$,
или $6\cdot 5=30$. В общем случае, если имеется $m$ возможностей для
одно событие и $n$ для второго события, количество возможных исходов
для обоих событий вместе равно $m\cdot n$.
Пример 1.2.1 Сколько исходов возможно при броске трех игральных костей, если не может быть двух одинаковых? Первые две кости вместе имеют $6\cdot 5=30$ возможных исходов, сверху. Для каждого из этих 30 исходов, есть четыре возможных исхода для третьего кубика, поэтому общее количество исходов $30\cdot 4=6\cdot 5\cdot 4=120$. (Обратите внимание, что мы считаем кости различимыми, то есть броском 6, 4, 1 отличается от 4, 6, 1, потому что первое и второе кости различны в двух бросках, даже несмотря на то, что числа как набор одинаковы.) $\квадрат$
Пример 1.2.2. Предположим, что блоки с номерами от 1 до $n$ находятся в бочке; мы вытащите из них $k$, расположив их в линию, как мы. Сколько исходы возможны? То есть, сколько различных расположений $k$ блоки могли бы мы видеть?
По сути, это то же самое, что и в предыдущем примере: имеется $k$ «пятен».
заполняться блоками. Любой из блоков $n$ может появиться первым в
линия; то любой из оставшихся $n-1$ может появиться следующим, и, таким образом,
на.
Таким образом, число исходов равно $n(n-1)(n-2)\cdots(n-k+1)$, согласно
принцип умножения. в
В предыдущем примере первое «пятно» было номером один, второе
точка была номером два, третья точка была номером три, и
$6\cdot5\cdot4=6(6-1)(6-2)$; обратите внимание, что $6-2=6-3+1$.
$\квадрат$
Это довольно общая проблема:
Определение 1.2.3 Количество перестановок $n$ вещи, взятые $k$ за раз, $$P(n,k)=n(n-1)(n-2)\cdots(n-k+1)={n!\over (n-k)!}.$$ $\квадрат$
Перестановка некоторых объектов представляет собой конкретное линейное упорядочение
объекты; Фактически $P(n,k)$ одновременно учитывает две вещи:
количество способов выбрать и упорядочить $k$ из $n$ объектов. Полезный
частный случай $k=n$, в котором мы просто считаем число
способов упорядочить все $n$ объектов. Это
$n(n-1)\cdots(n-n+1)=n!$. Обратите внимание, что вторая форма $P(n,k)$ из
определение дает
$${n!\over (n-n)!}={n!\over 0!}.$$
Это правильно, только если $0!=1$, поэтому мы принимаем стандартное соглашение
что это правда, то есть мы определяет $0!$ как $1$.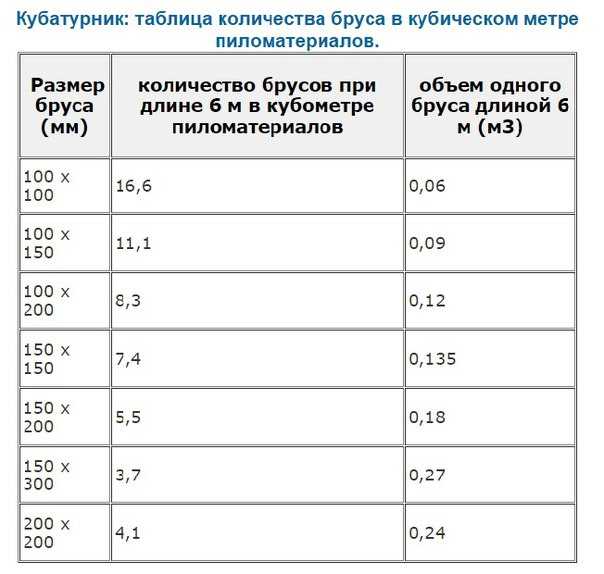
Предположим, мы хотим подсчитать только количество способов выбрать $k$ предметов. из $n$, то есть порядок нам не важен. В Пример 1.2.1, мы подсчитали количество броски трех игральных костей с разными числами. Кости были различимы или в определенном порядке: первый кубик, второй и третий. Теперь мы хотим просто посчитать, сколько комбинаций чисел есть, причем 6, 4, 1 теперь считаются той же комбинацией, что и 4, 6, 1.
Пример 1.2.4
Предположим, нам нужно перечислить все 120 возможностей в
пример 1.2.1. Список будет содержать
множество исходов, которые мы теперь хотим считать одним исходом;
6, 4, 1 и 4, 6, 1 будут в списке, но не должны учитываться
в отдельности. Сколько раз один результат появится в списке?
Это задача на перестановку: есть $3!$ порядков, в которых 1, 4, 6
может появиться, и все 6 из них будут в списке. На самом деле каждый
исход появится в списке 6 раз, так как каждый исход может
появляются в заказах $3!$. Следовательно, список слишком велик в 6 раз;
правильный счет для новой задачи: $120/6=20$.
$\квадрат$
Следуя тем же рассуждениям вообще, если у нас есть $n$ объектов, количество способов выбрать $k$ из них $P(n,k)/k!$, так как каждый набор из $k$ объектов будет посчитал $k!$ раз по $P(n,k)$.
Определение 1.2.5 Количество подмножеств размера $k$ множества размера $n$ (также называется $n$-множеством) $$C(n,k)={P(n,k)\более k!}={n!\over k!(n-k)!}={n\выбрать k}.$$ Обозначение $C(n,k)$ используется редко; вместо этого мы используем $n\выбрать k$, произносится как «$n$ выбирает $k$». $\квадрат$
Пример 1.2.6
Рассмотрим $n=0,1,2,3$. Несложно перечислить
подмножества малого $n$-множества; типичное $n$-множество
$\{a_1,a_2,\ldots,a_n\}$.
$0$-множество, а именно пустое множество, имеет
одно подмножество, пустой набор; $1$-множество имеет два подмножества, пустое множество
и $\{a_1\}$; $2$-подмножество имеет четыре подмножества, $\emptyset$, $\{a_1\}$,
$\{a_2\}$, $\{a_1,a_2\}$; а $3$-подмножество имеет восемь:
$\emptyset$, $\{a_1\}$, $\{a_2\}$, $\{a_3\}$, $\{a_1,a_2\}$,
$\{a_1,a_3\}$, $\{a_2,a_3\}$, $\{a_1,a_2,a_3\}$.
Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
Вы, наверное, узнаете эти цифры: это начало Треугольник Паскаля . Каждая запись в Треугольник Паскаля получается путем добавления двух элементов из предыдущего ряд: тот, что прямо сверху, и тот, что выше и левее. Этот предполагает, что ${n\выбрать k}={n-1\выбрать k-1}+{n-1\выбрать k}$, и действительно это правда. Чтобы сделать это аккуратно, мы принимаем соглашение о том, что ${n\choose k}=0$, когда $kn$.
Теорема 1.2.7 $\ds{n\выберите k}={n-1\выберите k-1}+{n-1\выберите k}$.
Доказательство. Типичным $n$-множеством является $A=\{a_1,\ldots,a_n\}$. Мы рассматриваем два типа
подмножества: содержащие $a_n$ и не содержащие. Если
$k$-подмножество $A$ не содержит $a_n$, то оно является $k$-подмножеством
$\{a_1,…,a_{n-1}\}$, и таких $n-1\выберите k$.
Если оно
содержит $a_n$, то он состоит из $a_n$ и $k-1$ элементов
$\{a_1,…,a_{n-1}\}$; так как их $n-1\выберите k-1$,
таких подмножеств $n-1\выберите k-1$. Таким образом, общее количество
$k$-подмножеств $A$ равно ${n-1\выбрать k-1}+{n-1\выбрать k}$.
Обратите внимание, что когда $k=0$, ${n-1\выберите k-1}={n-1\выберите -1}=0$, и когда $k=n$, ${n-1\выбрать k}={n-1\выбрать n}=0$, так что ${n\выбрать 0}={n-1\выбрать 0}$ и ${n\выбрать n}={n-1\выбрать п-1}$. Эти значения являются граничными в треугольнике Паскаля. $\qed$
Многие проблемы со счетом основаны на рассуждениях, которые у нас есть. видимый. Вот несколько вариаций на тему.
Пример 1.2.8 Шесть человек должны сидеть за круглым столом; сколько сидячих мест аранжировки есть?
Не совсем ясно, что именно мы имеем в виду, чтобы считать здесь. если есть
«специальное место», например, может иметь значение, кто окажется на этом
сиденье. Если это не имеет значения, нас интересует только относительное положение
каждого человека.
Тогда может или не может быть важно, является ли определенное лицо
находится слева или справа от другого. Так что этот вопрос можно
интерпретируется (по крайней мере) тремя способами. Давайте ответим на них все.
Во-первых, если имеют значение фактические стулья, на которых сидят люди, то это
точно так же, как выстраивание шести человек в ряд: 6 вариантов места
номер один, 5 для второго места и так далее, всего 6 долларов! Если
стулья не имеют значения, тогда $6!$ считают одно и то же расположение слишком большим
раз, по одному разу для каждого человека, который может быть на первом месте. Итак, общее количество в
в этом случае $6!/6=5!$. Другой подход к этому: поскольку фактическое
места не имеют значения, просто посадите одного из шести человек на стул. Тогда мы
нужно расставить оставшихся 5 человек в ряд, что можно сделать в
$5!$ способами. Наконец, предположим, что нас волнует только то, кто рядом с кем,
игнорируя право и лево. Тогда предыдущий ответ считает каждый
расположение дважды, один раз для порядка против часовой стрелки и один раз для
по часовой стрелке.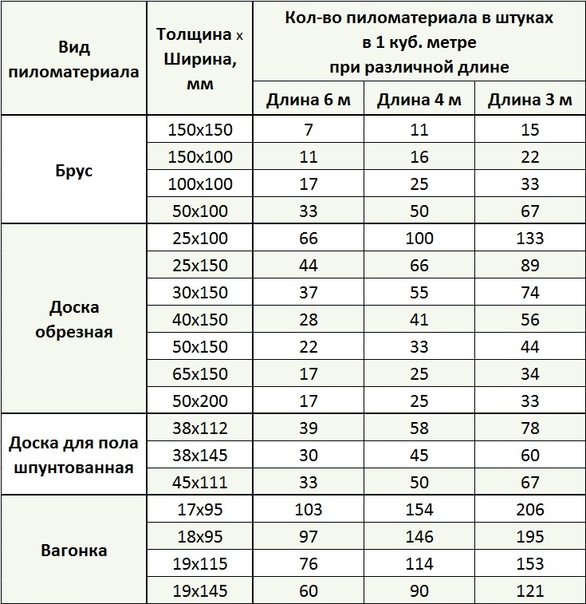
Итого $5!/2=P(5,3)$.
$\квадрат$
Мы дважды видели общий принцип в действии: если мы можем пересчитать желаемый набор таким образом, чтобы каждый элемент считался одинаковым количество раз, мы можем получить желаемое количество, просто разделив на общий фактор пересчета. Это по-прежнему будет полезной идеей. А вариация на эту тему состоит в том, чтобы пересчитать , а затем вычесть из сумма перерасчета.
Пример 1.2.9. Сколькими способами можно выстроить шесть человек так, чтобы конкретная пара людей не является соседней?
Обозначим людей $A$ и $B$.
Общее количество заказов составляет $6!$, но здесь учитываются заказы с
$A$ и $B$ рядом друг с другом. Сколько из них есть? Думать о
эти два человека как единое целое; сколько существует способов выстроить
Блок $AB$ с остальными четырьмя людьми? У нас есть 5 предметов, поэтому ответ
$5!$. Каждый из этих порядков соответствует двум различным порядкам в
которые $A$ и $B$ являются смежными, в зависимости от того, является ли $A$ или $B$
первый.
Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Пример 1.2.2 Покерная рука состоит из пяти карт из стандартных 52 карт. колода с четырьмя мастями и тринадцатью достоинствами в каждой масти; получатель чего-то карты в руке значения не имеют. Из скольких рук состоит 2 карты одного достоинства и 3 карты другого достоинства (фулл-хаус)? Сколько состоит из 5 карт одной масти (флеш)?
Пример 1.2.3 Шестеро мужчин и шесть женщин должны сидеть за столом, мужчины и женщины чередуются. Стулья не имеют значения, важно только, кто следующий кому, а правое и левое разные. Сколько сидячих мест аранжировки возможны?
Пример 1.2.4 Восемь человек должны сидеть за столом; стулья неважно, только кто рядом с кем, а справа и слева другой. Два человека, X и Y, не могут сидеть рядом друг с другом. Сколько посадочных мест возможно?
Пример 1.
2.5 В шахматах ладья атакует любую фигуру в той же строке или столбце.
как ладья, если между ними нет другой фигуры. Сколькими способами
можно ли разместить на шахматной доске восемь неразличимых ладей так, чтобы
двое не нападают друг на друга? Как насчет восьми неразличимых ладей на
доска $10\times 10$?
Пример 1.2.6 Предположим, мы хотим поставить 8 неатакующих ладей на поле. шахматная доска. Сколькими способами мы можем это сделать, если 16 наиболее Квадраты «северо-запад» должны быть пустыми? А если только 4 самых Квадраты «северо-запад» должны быть пустыми?
Пример 1.2.7 «Правильная» последовательность скобок — это последовательность, в которой скобки
могут быть правильно сопоставлены, например $()(())$. Нетрудно заметить, что это
возможно именно тогда, когда число левых и правых скобок равно
то же самое, и каждый начальный сегмент последовательности имеет по крайней мере как
многие левые скобки как правые. Например, $())\ldots$ не может
возможно, будет расширена до юридической последовательности.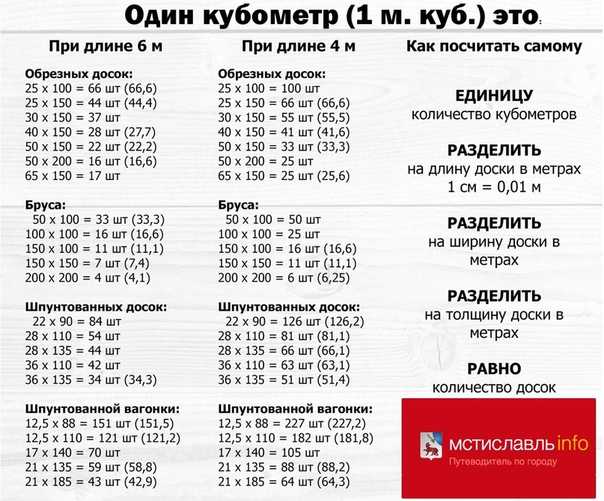
Покажите, что количество
допустимые последовательности длины $2n$ равны $C_n={2n\выбрать n}-{2n\выбрать n+1}$.
Числа $C_n$ называются Каталонский
номера .
| 1,0 Ватт (Вт) | 1 Джоулей (Дж) в секунду | |
| 1,0 Гигаджоули (ГДж) | 1 x 10 9 Джоули (Дж) | |
| 1,0 гигаджоулей (ГДж) | 0,9478 миллион британских тепловых единиц (MMBtu) | |
| 1,0 Гигаджоули (ГДж) | 2,7778 x 10 5 Ватт-часы (Вт-ч) | |
| 1,0 Гигаджоули (ГДж) | 277,7778 Киловатт-часы (кВт.ч) | |
| 1,0 Гигаджоули (ГДж) | 0,2778 Мегаватт-часы (МВт.ч) | |
| 1,0 Гигаджоули (ГДж) | 2,7778 x 10 -4 Гигаватт-часы (ГВт. ч) | |
| 1,0 Гигаджоули (ГДж) | 2,7778 x 10 -7 Тераватт-часы (ТВ.ч) | |
| 1,0 Гигаджоули (ГДж) | 947,8171 Кубические футы (cf) природного газа | |
| 1,0 Гигаджоули (ГДж) | 26,853 Кубические метры (м³) природного газа | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 1,0551 x 10 9 Джоули (Дж) | |
| 1,0 Миллионы британских тепловых единиц (MMBtu) | 1,0551 Гигаджоули (ГДж) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 2,9307 x 10 5 Ватт-часы (Вт-ч) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 293,0711 Киловатт-час (кВт. ч) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 0,2931 Мегаватт-час (МВт·ч) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 2,9307 x 10 -4 Гигаватт-час (ГВт.ч) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 2,9307 Тераватт-час (ТВ.ч) | |
| 1,0 Миллион британских тепловых единиц (MMBtu) | 1 000 Кубических футов (cf) природного газа | |
| 1,0 миллионов британских тепловых единиц (MMBtu) | 28,3278 кубических метров (м³) | |
| 1,0 Ватт-часы (Вт.ч) | 3600 Джоули (Дж) | |
| 1,0 Ватт-часы (Втч) | 3,6 x 10 -6 Гигаджоули (ГДж) | |
| 1,0 Ватт-часы (Вт·ч) | 3,4121 x 10 -6 Миллион британских тепловых единиц (MMBtu) | |
1,0 Ватт-часы (Вт.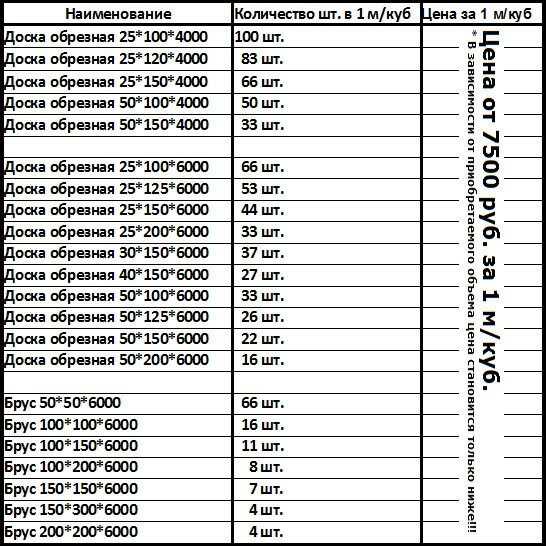 ч) | 1 x 10 -3 Киловатт-часы (кВт.ч) | |
| 1,0 Ватт-часы (Вт.ч) | 1 x 10 -6 Мегаватт-часы (МВт-ч) | |
| 1,0 Ватт-часы (В.ч) | 1 x 10 -9 Гигаватт-часы (ГВт.ч) | |
| 1,0 ватт-часы (Вт.ч) | 1 x 10 -12 тераватт-часы (ТВт.ч) | |
| 1,0 Киловатт-часы (кВт.ч) | 3,6 x 10 6 Джоули (Дж) | |
| 1,0 Киловатт-часы (кВт.ч) | 3,6 x 10 -3 Гигаджоули (ГДж) | |
| 1,0 Киловатт-час (кВт·ч) | 3,4121 x 10 -3 Миллион британских тепловых единиц (MMBtu) | |
1,0 Киловатт-часы (кВт. ч) | 1 000 Ватт-часы (Вт.ч) | |
| 1,0 Киловатт-час (кВт·ч) | 1 x 10 -3 Мегаватт-час (МВт·ч) | |
| 1,0 Киловатт-часы (кВт.ч) | 1 x 10 -6 Гигаватт-часы (ГВт.ч) | 1 x 10 |
| 1,0 Мегаватт-часы (МВт.ч) | 3,6 x 10 9 Джоули (Дж) | |
| 1,0 Мегаватт-часы (МВт.ч) | 3,60 Гигаджоули (ГДж) | |
| 1,0 Мегаватт-часы (МВт·ч) | 3,4122 Миллион британских тепловых единиц (MMBtu) | |
| 1,0 Мегаватт-часы (МВт.ч) | 1 x 10 6 | |
| 1,0 Мегаватт-часы (МВт.ч) | 1000 Киловатт-часы (кВт. ч) | |
| 1,0 Мегаватт-часы (МВт.ч) | 1 x 10 -3 Гигаватт-часы (ГВт·ч) | |
| 1,0 Мегаватт-часы (МВт.ч) | 1 x 10 -6 Тераватт-часы (ТВт.ч) | |
| 1,0 Гигаватт-часы (ГВт.ч) | 3,6 x 10 12 Джоули (Дж) | |
| 1,0 Гигаватт-часы (ГВт.ч) | 3600 Гигаджоули (ГДж) | |
| 1,0 Гигаватт-часы (ГВт.ч) | 3 412,1416 Миллион британских тепловых единиц (MMBtu) | |
| 1,0 Гигаватт-часы (ГВт.ч) | 1 x 10 9 | |
| 1,0 Гигаватт-часы (ГВт.ч) | 1 x 10 6 Киловатт-часы (кВт.ч) | |
| 1,0 Гигаватт-час (ГВт·ч) | 1 000 Мегаватт-час (МВт·ч) | |
1,0 Гигаватт-часы (ГВт. ч) | 1 x 10 -3 Тераватт-часы (ТВт.ч) | |
| 1,0 Тераватт-часы (ТВт.ч) | 3,6 x 10 15 Джоули (Дж) | |
| 1,0 Тераватт-часы (ТВт.ч) | 3,6 x 10 6 Гигаджоули (ГДж) | |
| 1,0 Тераватт-часы (ТВт.ч) | 3,4121 x 10 6 Миллион британских тепловых единиц (MMBtu) | |
| 1,0 Тераватт-часы (ТВт.ч) | 1 x 10 12 Ватт-часы (Вт.ч) | |
| 1,0 Тераватт-часы (ТВт.ч) | 1 x 10 9 Киловатт-часы (кВтч) | |
| 1,0 Тераватт-часы (ТВт.ч) | 1 x 10 6 Мегаватт-часы (МВт.ч) | |
1,0 Тераватт-часы (ТВт. |