|
Random converter |
Калькулятор мощности трехфазного переменного токаЭтот калькулятор мощности трехфазного тока позволяет определить активную, полную и реактивную мощность по известным среднеквадратичным значениям напряжения, тока и коэффициенту мощности в системе с симметричным трехфазным напряжением и равномерной нагрузкой. Пример: Три равных индуктивных нагрузки с коэффициентом мощности 0,68 подключены звездой к сети с линейным напряжением 400 В 50 Гц. Ток каждой фазы 10 А. Рассчитать активную и реактивную нагрузку на каждой фазе, фазное напряжение, фазный ток, фазовый угол, линейный ток, активную, реактивную и полную мощность. Тип расчетов:Мощность и ток по напряжение и нагрузке Мощность и нагрузка по напряжению и току Входные данные Тип соединения Звезда (Y)Треугольник (Δ) Среднеквадратичное значение напряженияЛинейное напряжение UL rmsвольт (В)киловольт (кВ)мегавольт (МВ) Среднеквадратичное значение напряжения между линейными проводами (напряжение между фазами) в симметричной трехфазной системе. или Фазное напряжение Uph rmsвольт (В)киловольт (кВ)мегавольт (МВ) Среднеквадратичное значение напряжения на каждой фазе симметричной трехфазной системы относительно нейтрали. Импеданс нагрузки в каждой фазеАктивное сопротивление нагрузки в каждой фазе Rphмиллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм) Реактивное сопротивление нагрузки в каждой фазе Xph Ом Zph= Rph + jXph= R + jXОм ИЛИ Величина (модуль) импеданса нагрузки |Z|phмиллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм) Фазовый угол импеданса нагрузки φphградус (°)радиан (рад) Zph= |Z|ph ∠φph= |Z| ∠φ° Ом Вначале выберите тип расчёта. Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Полная мощность по всем трем фазам |S| ГВ·А Полная активная мощность P Вт Полная реактивная мощность Q Вар Полная комплексная мощность S ГВ·А Среднеквадратичное значение фазного тока Iph RMS А Среднеквадратичное значение линейного тока IL RMS А Фазовый сдвиг φ ° рад Коэффициент мощности PF Дано Найти Решение Однофазный и трехфазный ток Определения и формулы Генерация трехфазного тока Преимущества трехфазных систем Последовательность фаз Фазное напряжение и фазный ток Линейное напряжение и ток Симметричные и несимметричные системы и нагрузки Линейные и нелинейные нагрузки Соединение треугольником и звездой Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездой Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольником Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощности Импеданс нагрузки Z Расчет тока и мощности по известным напряжению и нагрузке Фазный ток Преобразование из прямоугольных координат в полярные и наоборот Активное Rph и реактивное Xph сопротивление нагрузки Импеданс конденсатора и катушки индуктивности Параллельная нагрузка RLC Последовательная нагрузка RLC Примеры расчетов Пример 1. Пример 2. Расчет мощности и тока по заданным напряжению и нагрузке Пример 3. Расчет мощности и тока по заданным напряжению и нагрузке Пример 4. Расчет мощности и нагрузки по заданным напряжению и току Пример 5. Расчет мощности и тока по заданным напряжению и нагрузке Пример 6. Расчет мощности и тока по заданным напряжению и нагрузке Пример 7. Расчет мощности и нагрузки по заданным напряжению и току Однофазную сеть можно сравнить с проселочной дорогой — оно не позволяет получить большую мощность. Трехфазную сеть можно сравнить с автомагистралью — она обычно имеется в промышленных зданиях для питания оборудования большой мощности Установленный на столбе однофазный трансформатор, предназначенный для подачи электроэнергии в индивидуальные жилые дома (Канада) Термин «фаза» относится к распределению электрической энергии. Для далеких от физики людей однофазную и трехфазную сеть можно сравнить с иллюстрациями выше. В однофазной сети используются два или три провода. Всегда имеется один фазный провод и один провод, называемый нейтралью или нулевым проводом. Ток течет между этими двумя проводами. Если однофазная сеть содержит заземляющий провод, то используется трехпроводная сеть. Однофазная сеть хороша в тех случаях, когда типичными нагрузками являются чисто активные потребители, например, традиционные лампы накаливания и электрические обогреватели. Установленная на столбе группа из трех трансформаторов, обеспечивающая трехфазное питание небольшой промышленной установки В трехфазной сети используются три провода, называемые фазными или просто фазами. По этим проводам текут синусоидальные токи со сдвигом фаз относительно друг друга на 120°. В трехфазной системе может быть три или четыре провода. Если имеется четвертый провод, то трехфазную сеть можно использовать для подачи однофазного питания (три линии), например, в индивидуальные жилые дома. При этом от каждой фазы в нагрузку (дом) подается примерно одинаковая мощность. Нейтральный провод часто имеет меньшее сечение, потому что фазные токи взаимно гасятся и по нейтральному проводу обычно течет совсем небольшой ток. Трехфазная система обеспечивает постоянную передачу мощности в нагрузку, что позволяет подключить более высокую нагрузку. Определения и формулыГенерация трехфазного токаВ простейшем трехфазном генераторе имеется три идентичных обмотки, расположенных под углом 120° по отношению друг к другу. Здесь Up — пиковое значение (амплитуда) напряжения в вольтах, ω — угловая частота в радианах в секунду и t — время в секундах. Напряжение, наведенное в обмотке 2, отстает от напряжения в обмотке 1 на 120°, а напряжение, наведенное в обмотке 3, отстает от напряжения в обмотке 1 на 240°. Ниже на рисунке приведены векторные диаграммы и формы колебаний напряжений генератора: Если коэффициент мощности равен единице, то в каждой фазе трехфазной системы напряжение, ток и мощность сдвинуты относительно друг друга на 120°; последовательность фаз на этом рисунке U₁, U₂, U₃, потому что U₁ опережает U₂, U₂ опережает U₃, и U₃ опережает U₁. Преимущества трехфазных систем
Последовательность фазПоследовательность фаз определяется временем, при котором напряжения трех фаз достигают положительного максимума. Последовательность фаз называют также порядком фаз. На рисунке выше последовательность фаз 1-2-3, так как фаза 1 достигает положительного максимума раньше, чем фаза 2, а фаза 3 достигает положительного максимума позже фазы 2. Для определения порядка фаз на векторной диаграмме нужно знать, что векторы всегда вращаются против часовой стрелки. Например, на этих трех чертежах последовательность чередования фаз снова U₁, U₂, U₃: Фазное напряжение и фазный токФазным называется напряжение между каждым из трех фазных проводов и нейтралью. Его также называют напряжением между фазой и нейтралью. Ток, которые течет в нагрузке между фазным проводом и нейтралью, называется фазным током. Линейное напряжение и токЛинейным называется напряжение между любыми двумя фазами (линиями). Ток, протекающий в каждой из линий, называется линейным. Симметричные и несимметричные системы и нагрузкиВ сбалансированной (симметричной) трехфазной системе токи во всех трех фазах равны, а сумма всех токов равна нулю, поэтому ток по нейтрали не течет. То же можно сказать и о токах в симметричной системе: Если три нагрузки, присоединенные к трем линиям, имеют одинаковую величину и коэффициент мощности, она также называются сбалансированными или симметричными. Линейные и нелинейные нагрузкиВ линейных нагрузках в цепях переменного тока напряжения и токи имеют синусоидальную форму и в любое время ток в нагрузке прямо пропорционален напряжению на ней. Примерами линейных нагрузок являются нагреватели, лампы накаливания. конденсаторы и катушки индуктивности. Все линейные нагрузки подчиняются закону Ома. В линейных нагрузка коэффициент мощности равен cos φ. Подробнее о нелинейных нагрузках — в нашем Калькуляторе активной и реактивной мощности. В нелинейных нагрузках ток не пропорционален напряжению и содержит гармоники основной частоты 50 или 60 Гц. Соединение треугольником и звездойТри обмотки трехфазного генератора можно присоединить к нагрузке шестью проводами, по два на обмотку. Для уменьшения количества проводов обмотки присоединяются к нагрузке тремя или четырьмя проводами. Эти два способа подключения называются треугольником (Δ) и звездой (Y). В соединении треугольником начало каждой обмотки соединяется с концом следующей обмотки. Таким образом энергию можно передавать только по трем проводам. Соединение звездой (слева) и треугольником (справа) В симметричной соединении треугольником напряжения равны по амплитуде, отличаются по фазе на 120° и их сумма равна нулю: В симметричной четырехпроводной системе соединения звездой с тремя одинаковыми подключенными к каждой фазе нагрузками мгновенное значение тока, текущего по нейтрали, равно сумме трех фазных токов i₁, i₂, и i₃, которые имеют одинаковые амплитуды Ip и сдвинуты по фазе на 120°: Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездойСоединение звездой; I₁, I₂, и I₃ — фазные токи, которые равны линейным токам Полная мощность в трехфазной системе является суммой мощностей, потребляемых нагрузками в каждой из трех фаз. Здесь φ — разность фаз между током и напряжением. Поскольку в трехфазном соединении звездой фазное Uph и линейное среднеквадратичное напряжение UL связаны как а среднеквадратичное значения линейного и фазного токов равны полная активная мощность определяется следующим уравнением: Полная реактивная мощность равна Комплексная мощность: И, наконец, полная мощность в трех фазах определяется формулой: Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольникомСоединение треугольником; I13, I23, и I32 — фазные токи, а I1, I2, и I3 — линейные токи; при этом IL = √3∙Iph При соединении треугольником нейтральный проводник отсутствует и конец одной обмотки генератора соединяется с началом следующей обмотки. При соединении треугольником фазные токи — это токи, текущие через фазные нагрузки. Мы рассматриваем симметричную систему, поэтому фазные среднеквадратичные значения токов Ip1, Ip2 и Ip3 по амплитуде равны (Ip) и отличаются по фазе на 120°: Как мы уже упоминали, общая мощность в трехфазной системе — это сумма мощностей, потребляемых в нагрузках трех фаз: где φ — сдвиг фаз между током и напряжением. Поскольку при соединении треугольником среднеквадратичные значения фазного Uph и линейного напряжений UL равны, а среднеквадратичные значения линейного и фазного токов связаны формулой активная мощность определяется следующим уравнением: Полная реактивная мощность равна Комплексная мощность: И полная мощность в трех фазах: Отметим, что приведенные выше уравнения для мощности при соединении звездой и треугольником одинаковые. То, что эти формулы мощности для звезды и треугольника одинаковые, иногда приводит к ошибочным выводам о том, что можно соединить обмотки одного и того же электродвигателя звездой или треугольником и потребляемая мощность (и ток!) не изменятся. Конечно, это неправильно. И если мы в калькуляторе соединение звездой изменим на треугольник, не изменяя нагрузку, мы увидим, что мощность и потребляемый ток изменятся. Рассмотрим пример. Трехфазный электродвигатель подключен по схеме треугольника и работает на полной номинальной мощности при линейном напряжении UL и линейном токе IL. Полная мощность в вольт-амперах (ВА) равна Затем обмотки того же двигателя соединили звездой. Линейное напряжение, приложенное к каждой обмотке, уменьшилось в 1/1,73 раза, при этом сетевое напряжение осталось прежним. Ток в каждой обмотке уменьшился в 1/1,73 раза по сравнению с током, потребляемым при соединении треугольником. Таким образом, полная мощность при соединении звездой равна одной трети мощности при соединении треугольником для нагрузки с тем же импедансом. Очевидно, что полный момент двигателя, обмотки которого соединены звездой, будет в три раза меньше момента того же двигателя при соединении обмоток треугольником. Иными словами, хотя новая мощность для соединения звездой рассчитывается по той же формуле, что и для треугольника, в расчет нужно вставить другие величины, а именно, напряжение и ток. уменьшенные в 1,73 раза (то есть в квадратный корень из 3). Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощностиДля расчета симметричной нагрузки (одинаковой в каждой фазе) по известным напряжению, току и коэффициенту мощности (опережающему или отстающему) используются следующие формулы: Импеданс нагрузкиZВ полярной форме: В комплексной форме: Расчет тока и мощности по известным напряжению и нагрузкеФазный токПо закону Ома, имеем: Преобразование из прямоугольных координат в полярные и наоборотДля преобразования из прямоугольных координат R, X в полярные координаты |Z|, φ, используйте следующие формулы: Треугольник импеданса В этих формулах R всегда положительно, а X положительно для индуктивной нагрузки (ток отстает от напряжения) и отрицательно для емкостной нагрузки (ток опережает напряжение). Преобразование из полярных координат r, φ в прямоугольные coordinates x, y, выполняется по формулам: АктивноеRph и реактивное Xph сопротивление нагрузкиИмпеданс конденсатора и катушки индуктивностиПараллельная нагрузка RLCПараллельное соединение RLC Для расчета используйте наш Калькулятор импеданса параллельной RLC-цепи. Последовательная нагрузка RLCПоследовательное соединение RLC Для расчета используйте наш Калькулятор импеданса последовательной RLC-цепи Более подробную информацию о нагрузки в форме RLC-цепи вы найдете в наших калькуляторах для расчета импеданса:
Примеры расчетовПример 1. Расчет мощности и тока по заданным напряжению и нагрузке Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех цепей с равными импедансами Zph = 5+j3 Ом подключена звездой к трехфазной сети с линейным напряжением 400 В 50 Гц. Рассчитать фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 2. Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех цепей с равными импедансами Zph = 15 ∠60° Ом подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 110 В 50 Гц. Определить тип нагрузки (емкостная или индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 3. Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех обмоток с равными импедансами и эквивалентной схемой в виде включенных последовательно сопротивления Rph = 20 Ом и индуктивности Lph = 440 мГн подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 230 В 50 Гц. Рассчитайте фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Найти линейный ток и потребляемую мощность для той же нагрузки, но соединенной треугольником. Совет: Для определения импеданса каждой обмотки воспользуйтесь Калькулятором последовательной RL-цепи. Пример 4. Расчет мощности и нагрузки по заданным напряжению и токуСимметричный трехфазный генератор подает фазное напряжение 230 В на включенную звездой нагрузку с отстающим (активно-индуктивным) коэффициентом мощности 0,75. Пример 5. Расчет мощности и тока по заданным напряжению и нагрузкеНагрузка, состоящая из трех одинаковых обмоток, имеющих сопротивление Rph = 10 Ом и индуктивность Lph = 310 мГн, подключена треугольником к трехфазной сети с напряжением между фазой и нейтралью 120 В, 60 Гц. Рассчитайте линейное напряжение UL, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 6. Расчет мощности и тока по заданным напряжению и нагрузкеНагрузка из трех цепей с равными импедансами Zph = 7 – j5 Ом подключена треугольником к трехфазной сети с линейным напряжением (между двумя фазами) 208 В 60 Гц. Определить тип нагрузки (резистивно-емкостная или резистивно-индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 7. Расчет мощности и нагрузки по заданным напряжению и токуСимметричная нагрузка подключена звездой к симметричному трехфазному генератору с линейным (между двумя фазами) напряжением 208 В 60 Гц. Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:Калькулятор резистивно-емкостной цепи Калькулятор параллельных сопротивлений Калькулятор параллельных индуктивностей Калькулятор емкости последовательного соединения конденсаторов Калькулятор импеданса конденсатора Калькулятор импеданса катушки индуктивности Калькулятор взаимной индукции Калькулятор взаимоиндукции параллельных индуктивностей Калькулятор взаимной индукции — последовательное соединение индуктивностей Калькулятор импеданса параллельной RC-цепи Калькулятор импеданса параллельной LC-цепи Калькулятор импеданса параллельной RL-цепи Калькулятор импеданса параллельной RLC-цепи Калькулятор импеданса последовательной RC-цепи Калькулятор импеданса последовательной LC-цепи Калькулятор импеданса последовательной RL-цепи Калькулятор импеданса последовательной RLC-цепи Калькулятор аккумуляторных батарей Калькулятор литий-полимерных аккумуляторов для дронов Калькулятор индуктивности однослойной катушки Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC) Калькулятор расчета параметров коаксиальных кабелей Калькулятор светодиодов. Калькулятор цветовой маркировки резисторов Калькулятор максимальной дальности действия РЛС Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС Калькулятор радиогоризонта Калькулятор эффективной площади антенны Симметричный вибратор Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации Калькулятор мощности постоянного тока Калькулятор мощности переменного тока Калькулятор пересчета ВА в ватты Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую Калькулятор коэффициента гармонических искажений Калькулятор законов Ома и Джоуля — Ленца Калькулятор времени передачи данных Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора Калькуляторы Электротехнические и радиотехнические калькуляторы |
Пример расчета тока трехфазного к.
 з. в сети 0,4 кВ
з. в сети 0,4 кВСодержание
- 1. Определение сопротивлений питающей энергосистемы
- 2. Определение сопротивлений трансформатора 6/0,4 кВ
- 3. Определение сопротивлений шин
- 4. Определение сопротивлений кабеля
- 5. Определение сопротивлений трансформаторов тока
- 6. Определение сопротивлений автоматических выключателей
- 7. Определение сопротивлений контактных соединений кабелей и шинопроводов
- 8. Определение тока трехфазного к.з. в конце кабельной линии
- 9. Список литературы
В данном примере будет рассматриваться расчет тока трехфазного короткого замыкания в сети 0,4 кВ для схемы представленной на рис.1.
Исходные данные:
1. Ток короткого замыкания на зажимах ВН трансформатора 6/0,4 кВ составляет — 11 кА.
2. Питающий трансформатор типа ТМ — 400, основные технические характеристики принимаются по тех. информации на трансформатор:
- номинальная мощностью Sн.т — 400 кВА;
- номинальное напряжение обмотки ВН Uн.
 т.ВН – 6 кВ;
т.ВН – 6 кВ; - номинальное напряжение обмотки НН Uн.т.НН – 0,4 кВ;
- напряжение КЗ тр-ра Uк – 4,5%;
- мощность потерь КЗ в трансформаторе Рк – 5,5 кВт;
- группа соединений обмоток по ГОСТ 11677-75 – Y/Yн-0;
3. Трансформатор соединен со сборкой 400 В, алюминиевыми шинами типа АД31Т по ГОСТ 15176-89 сечением 50х5 мм. Шины расположены в одной плоскости — вертикально, расстояние между ними 200 мм. Общая длина шин от выводов трансформатора до вводного автомата QF1 составляет 15 м.
4. На стороне 0,4 кВ установлен вводной автомат типа XS1250CE1000 на 1000 А (фирмы SOCOMEC), на отходящих линиях установлены автоматические выключатели типа E250SCF200 на 200 А (фирмы SOCOMEC) и трансформаторы тока типа ТСА 22 200/5 с классом точности 1 (фирмы SOCOMEC).
5. Кабельная линия выполнена алюминиевым кабелем марки АВВГнг сечением 3х70+1х35.
Решение
Для того, чтобы рассчитать токи КЗ, мы сначала должны составить схему замещения, которая состоит из всех сопротивлений цепи КЗ, после этого, определяем все сопротивления входящие в цепь КЗ.
В практических расчетах для упрощения расчетов токов к.з. учитывается только индуктивное сопротивление энергосистемы, которое равно полному. Активное сопротивление не учитывается, данные упрощения на точность расчетов – не влияют!
1.1 Определяем сопротивление энергосистемы со стороны ВН по выражению 2-7 [Л1. с. 28]:
1.2 Определяем сопротивление энергосистемы приведенное к напряжению 0,4 кВ по выражению 2-6 [Л1. с. 28]:
2.1 Определяем полное сопротивление трансформатора для стороны 0,4 кВ по выражению 2-8 [Л1. с. 28]:
2.2 Определяем активное сопротивление трансформатора для стороны 0,4 кВ по выражению 2-9 [Л1. с. 28]:
2.3 Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по выражению 2-10 [Л1. с. 28]:
Для упрощения расчетов можно воспользоваться таблицей 2.4 [Л1. с. 28], как видно из результатов расчетов, активные и индуктивные сопротивления совпадают со значениями таблицы 2.
3.1 Определяем индуктивное сопротивление алюминиевых прямоугольных шин типа АД31Т сечением 50х5 по выражению 2-12 [Л1. с. 29]:
3.1.1 Определяем среднее геометрическое расстояние между фазами 1, 2 и 3:
3.2 По таблице 2.6 определяем активное погонное сопротивление для алюминиевой шины сечением 50х5, где rуд. = 0,142 мОм/м.
Для упрощения расчетов, значения сопротивлений шин и шинопроводов, можно применять из таблицы 2.6 и 2.7 [Л1. с. 31].
3.3 Определяем сопротивление шин, учитывая длину от трансформатора ТМ-400 до РУ-0,4 кВ:
4.1 Определяем активное и индуктивное сопротивление кабелей по выражению 2-11 [Л1. с. 29]:
Значения активных и индуктивных сопротивлений обмоток для одного трансформатора тока типа ТСА 22 200/5 с классом точности 1, определяем по приложению 5 таблица 20 ГОСТ 28249-93, соответственно r
Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.
Согласно [Л1. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.
Определяем активное сопротивление контактов по приложению 4 таблица 19 ГОСТ 28249-93:
- для рубильника на ток 1000 А – r
- для автоматического выключателя на ток 200 А — rав2 = 0,60 мОм.
Для упрощения расчетов, сопротивления контактных соединений кабелей и шинопроводов, я пренебрегаю, ввиду почти незаметного влияния на токи КЗ.
Если же вы будете использовать в своем расчете ТКЗ значения сопротивления контактных соединений кабелей и шинопроводов, то они принимаются по приложению 4 таблицы 17,18 ГОСТ 28249-93.
При приближенном учете сопротивлений контактов принимают:
- rк = 0,1 мОм — для контактных соединений кабелей;
- rк = 0,01 мОм — для шинопроводов.
8.1 Определяем ток трехфазного к.з. в конце кабельной линии:
1. Беляев А.В.
2. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
3. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
Всего наилучшего! До новых встреч на сайте Raschet.info.
пример расчета ТКЗ 0, расчет ткз в сети 0, сопротивление кабелей, сопротивление энергосистемы
Поделиться в социальных сетях
Трехфазный ток — простой расчет
К
Расчет тока в трехфазной системе был поднят на нашем сайте и является дискуссией, в которую я, кажется, участвую время от времени. В то время как некоторые коллеги предпочитают запоминать формулы или коэффициенты, я предпочитаю решать задачу шаг за шагом, используя базовые принципы. Я подумал, что было бы хорошо написать, как я делаю эти вычисления. Надеюсь, это может оказаться полезным для кого-то еще.
Я подумал, что было бы хорошо написать, как я делаю эти вычисления. Надеюсь, это может оказаться полезным для кого-то еще.
Трехфазная мощность и ток
Мощность, потребляемая цепью (однофазной или трехфазной), измеряется в ваттах Вт (или кВт). Произведение напряжения и тока представляет собой полную мощность и измеряется в ВА (или кВА). Соотношение между кВА и кВт представляет собой коэффициент мощности (pf):
что также может быть выражено как:
Однофазная система — с этим проще всего иметь дело. Учитывая мощность в кВт и коэффициент мощности, можно легко вычислить кВА. Ток — это просто кВА, деленное на напряжение. В качестве примера рассмотрим нагрузку, потребляющую мощность 23 кВт при напряжении 230 В и коэффициенте мощности 0,86:9.0008
Примечание: вы можете выполнить эти уравнения либо в ВА, В и А, либо в кВА, кВ и кА, в зависимости от величины параметров, с которыми вы имеете дело.
Чтобы преобразовать ВА в кВА, просто разделите на 1000.
Трехфазная система — Основное различие между трехфазной и однофазной системами заключается в напряжении. В трехфазной системе у нас есть линейное напряжение (V LL ) и фазное напряжение (V LN ), связанные:
или альтернативно как:
чтобы лучше понять это или получить больше информации, вы можете прочитать сообщение «Введение в трехфазную электроэнергию».
Для меня самый простой способ решения трехфазных задач — преобразовать их в однофазные задачи. Возьмем трехфазный двигатель (с тремя одинаковыми обмотками), потребляющий заданную мощность кВт. кВт на обмотку (однофазную) нужно разделить на 3. Точно так же трансформатор (с тремя обмотками, каждая из которых идентична), вырабатывающий заданное количество кВА, будет иметь каждую обмотку, обеспечивающую треть общей мощности. Чтобы преобразовать трехфазную проблему в однофазную, возьмите общее количество кВт (или кВА) и разделите на три.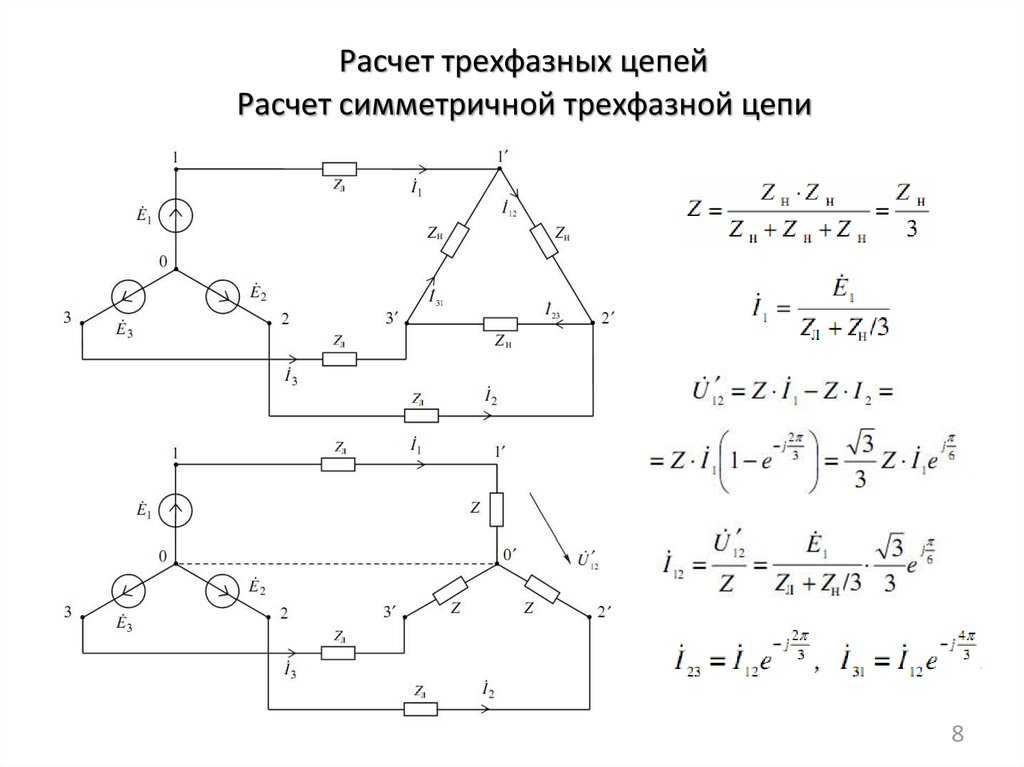
напряжение между фазой и нейтралью В LN = 400/√3 = 230 В
трехфазная мощность 36 кВт, однофазная мощность = 36/3 = 12 кВт
теперь просто следуйте описанному выше однофазному методу
Достаточно просто. Чтобы найти мощность при заданном токе, умножьте ее на напряжение, а затем на коэффициент мощности, чтобы преобразовать его в Вт. Для трехфазной системы умножьте ее на три, чтобы получить общую мощность.
Использование формулЛичная заметка о методе
Как правило, я запоминаю метод (не формулы) и переделываю его каждый раз, когда делаю расчет. Когда я пытаюсь запомнить формулы, я всегда быстро их забываю или не уверен, правильно ли я их запоминаю. Я бы посоветовал всегда помнить метод, а не просто запоминать формулу.
Конечно, если у вас есть какие-то сверхспособности к запоминанию формулы, вы всегда можете придерживаться этого подхода.
Вывод формулы – пример
Сбалансированная трехфазная система с общей мощностью P (Вт), коэффициентом мощности pf и линейным напряжением В 5 LL Преобразовать в проблема с одной фазой: Полная мощность одной фазы S 1-фазная (ВА): Фазный ток I (A) – полная мощность одной фазы, деленная на напряжение между фазой и нейтралью (при условии В LN = В LL / √3): Упрощая (и с 3 = √3 x √3): Приведенный выше метод основан на запоминании нескольких простых принципов и манипулировании задачей для получения ответа. Более традиционные формулы могут использоваться для получения того же результата. I=W3×pf×VLL, в A Вышеупомянутое относится к сбалансированным трехфазным системам. То есть ток в каждой фазе одинаков, и каждая фаза отдает или потребляет одинаковое количество энергии. Это характерно для систем передачи энергии, электродвигателей и подобного оборудования. Часто, когда используются однофазные нагрузки, например жилые и коммерческие помещения, система может быть несбалансированной, когда каждая фаза имеет разный ток и отдает или потребляет разное количество энергии. Сбалансированные напряжения К счастью, на практике напряжения имеют тенденцию быть фиксированными или очень небольшими. В этой ситуации и после небольшого размышления можно распространить вышеуказанный тип расчета на трехфазные системы с несимметричным током. Ключом к этому является то, что сумма мощностей в каждой фазе равна общей мощности системы. Например, возьмем трехфазную систему 400 В (V LL ) со следующими нагрузками: фаза 1 = 80 А, фаза 2 = 70 А, фаза 3 = 82 А напряжение между фазой и нейтралью В LN = 400/√3 = 230 В Точно так же, зная мощность в каждой фазе, можно легко найти фазные токи. Если вы также знаете коэффициент мощности, вы можете преобразовать кВА в кВт, как показано ранее. Несбалансированные напряжения Если напряжения становятся несимметричными или есть другие причины (например, несбалансированный фазовый сдвиг), необходимо вернуться к более традиционному анализу сети. Системные напряжения и токи можно найти, подробно нарисовав схему и используя законы Кирхгофа и другие сетевые теоремы. Сетевой анализ не является целью этой заметки. Если вас интересует введение, вы можете просмотреть нашу публикацию: Теория сетей — введение и обзор Другие факторы, которые необходимо учитывать при проведении расчетов, могут включать эффективность оборудования. Зная, что КПД энергопотребляющего оборудования — это выходная мощность, деленная на входную мощность, опять же это легко объяснить. Реактивная мощность в статье не обсуждается, более подробную информацию можно найти в других заметках (просто воспользуйтесь поиском по сайту). Помня, что трехфазная мощность (кВт или кВА) просто в три раза больше однофазной, любая трехфазная проблема может быть упрощена. Разделите кВт на коэффициент мощности, чтобы получить кВА. ВА — это просто произведение тока на напряжение, поэтому, зная это и напряжение, можно получить ток. При расчете тока используйте фазное напряжение, которое связано с линейным напряжением квадратным корнем из трех. К Стивен Макфадьен on Расчет тока в трехфазной системе был поднят на нашем сайте и является дискуссией, в которую я, кажется, участвую время от времени. В то время как некоторые коллеги предпочитают запоминать формулы или коэффициенты, я предпочитаю решать задачу шаг за шагом, используя базовые принципы. Я подумал, что было бы хорошо написать, как я делаю эти вычисления. Надеюсь, это может оказаться полезным для кого-то еще. Мощность, потребляемая цепью (однофазной или трехфазной), измеряется в ваттах Вт (или кВт). Произведение напряжения и тока представляет собой полную мощность и измеряется в ВА (или кВА). Однофазная система — с этим проще всего иметь дело. Учитывая мощность в кВт и коэффициент мощности, можно легко вычислить кВА. Ток — это просто кВА, деленное на напряжение. В качестве примера рассмотрим нагрузку, потребляющую мощность 23 кВт при напряжении 230 В и коэффициенте мощности 0,86:9.0008 Примечание: вы можете выполнить эти уравнения либо в ВА, В и А, либо в кВА, кВ и кА, в зависимости от величины параметров, с которыми вы имеете дело. Чтобы преобразовать ВА в кВА, просто разделите на 1000. Трехфазная система — Основное различие между трехфазной и однофазной системами заключается в напряжении. В трехфазной системе у нас есть линейное напряжение (V LL ) и фазное напряжение (V LN ), связанные: Для меня самый простой способ решения трехфазных задач — преобразовать их в однофазные задачи. Возьмем трехфазный двигатель (с тремя одинаковыми обмотками), потребляющий заданную мощность кВт. кВт на обмотку (однофазную) нужно разделить на 3. Точно так же трансформатор (с тремя обмотками, каждая из которых идентична), вырабатывающий заданное количество кВА, будет иметь каждую обмотку, обеспечивающую треть общей мощности. Чтобы преобразовать трехфазную проблему в однофазную, возьмите общее количество кВт (или кВА) и разделите на три. В качестве примера рассмотрим сбалансированную трехфазную нагрузку, потребляющую 36 кВт при коэффициенте мощности 0,86 и линейном напряжении 400 В (V LL ): напряжение между фазой и нейтралью В LN = 400/√3 = 230 В Достаточно просто. Личная заметка о методе Как правило, я запоминаю метод (не формулы) и переделываю его каждый раз, когда делаю расчет. Когда я пытаюсь запомнить формулы, я всегда быстро их забываю или не уверен, правильно ли я их запоминаю. Я бы посоветовал всегда помнить метод, а не просто запоминать формулу. Конечно, если у вас есть какие-то сверхспособности к запоминанию формулы, вы всегда можете придерживаться этого подхода. Вывод формулы – пример Сбалансированная трехфазная система с общей мощностью P (Вт), коэффициентом мощности pf и линейным напряжением В 5 LL Преобразовать в проблема с одной фазой: Полная мощность одной фазы S 1-фазная (ВА): Фазный ток I (A) – полная мощность одной фазы, деленная на напряжение между фазой и нейтралью (при условии В LN = В LL / √3): Упрощая (и с 3 = √3 x √3): Приведенный выше метод основан на запоминании нескольких простых принципов и манипулировании задачей для получения ответа. Более традиционные формулы могут использоваться для получения того же результата. Их можно легко получить из приведенного выше, например: I=W3×pf×VLL, в A Вышеупомянутое относится к сбалансированным трехфазным системам. То есть ток в каждой фазе одинаков, и каждая фаза отдает или потребляет одинаковое количество энергии. Это характерно для систем передачи энергии, электродвигателей и подобного оборудования. Часто, когда используются однофазные нагрузки, например жилые и коммерческие помещения, система может быть несбалансированной, когда каждая фаза имеет разный ток и отдает или потребляет разное количество энергии. Сбалансированные напряжения К счастью, на практике напряжения имеют тенденцию быть фиксированными или очень небольшими. В этой ситуации и после небольшого размышления можно распространить вышеуказанный тип расчета на трехфазные системы с несимметричным током. Например, возьмем трехфазную систему 400 В (V LL ) со следующими нагрузками: фаза 1 = 80 А, фаза 2 = 70 А, фаза 3 = 82 А напряжение между фазой и нейтралью В LN = 400/√3 = 230 В Точно так же, зная мощность в каждой фазе, можно легко найти фазные токи. Если вы также знаете коэффициент мощности, вы можете преобразовать кВА в кВт, как показано ранее. Несбалансированные напряжения Если напряжения становятся несимметричными или есть другие причины (например, несбалансированный фазовый сдвиг), необходимо вернуться к более традиционному анализу сети. Сетевой анализ не является целью этой заметки. Если вас интересует введение, вы можете просмотреть нашу публикацию: Теория сетей — введение и обзор Другие факторы, которые необходимо учитывать при проведении расчетов, могут включать эффективность оборудования. Зная, что КПД энергопотребляющего оборудования — это выходная мощность, деленная на входную мощность, опять же это легко объяснить. Реактивная мощность в статье не обсуждается, более подробную информацию можно найти в других заметках (просто воспользуйтесь поиском по сайту). Помня, что трехфазная мощность (кВт или кВА) просто в три раза больше однофазной, любая трехфазная проблема может быть упрощена. Разделите кВт на коэффициент мощности, чтобы получить кВА.
P1ph=P3
S1ph=P1phpf=P3×pf
I=S1phVLN=P3×pf3VLL
I=P3×pf×VLL Их можно легко получить из приведенного выше, например:
Их можно легко получить из приведенного выше, например:
Полная мощность фазы 1 = 80 x 230 = 18 400 ВА = 18,4 кВА
Полная мощность фазы 2 = 70 x 230 = 16 100 ВА = 16,1 кВА
Полная мощность фазы 3 = 82 x 230 = 18 860 ВА = 18,86 кВА
Общая трехфазная мощность = 18,4 + 16,1 + 18,86 = 53,36 кВА
Эффективность и реактивная мощность  Используя эти правила, можно решить любую трехфазную задачу без необходимости запоминать и/или прибегать к формулам.
Используя эти правила, можно решить любую трехфазную задачу без необходимости запоминать и/или прибегать к формулам. Трехфазный ток — простой расчет
 Соотношение между кВА и кВт представляет собой коэффициент мощности (pf):
Соотношение между кВА и кВт представляет собой коэффициент мощности (pf):
что также может быть выражено как:
или альтернативно как:
чтобы лучше понять это или получить больше информации, вы можете прочитать сообщение «Введение в трехфазную электроэнергию»
трехфазная мощность 36 кВт, однофазная мощность = 36/3 = 12 кВт
теперь просто следуйте описанному выше однофазному методу
 Чтобы найти мощность при заданном токе, умножьте ее на напряжение, а затем на коэффициент мощности, чтобы преобразовать его в Вт. Для трехфазной системы умножьте ее на три, чтобы получить общую мощность.
Чтобы найти мощность при заданном токе, умножьте ее на напряжение, а затем на коэффициент мощности, чтобы преобразовать его в Вт. Для трехфазной системы умножьте ее на три, чтобы получить общую мощность.
Использование формул
P1ph=P3
S1ph=P1phpf=P3×pf
I=S1phVLN=P3×pf3VLL
I=P3×pf×VLL
 Ключом к этому является то, что сумма мощностей в каждой фазе равна общей мощности системы.
Ключом к этому является то, что сумма мощностей в каждой фазе равна общей мощности системы.
Полная мощность фазы 1 = 80 x 230 = 18 400 ВА = 18,4 кВА
Полная мощность фазы 2 = 70 x 230 = 16 100 ВА = 16,1 кВА
Полная мощность фазы 3 = 82 x 230 = 18 860 ВА = 18,86 кВА
Общая трехфазная мощность = 18,4 + 16,1 + 18,86 = 53,36 кВА Системные напряжения и токи можно найти, подробно нарисовав схему и используя законы Кирхгофа и другие сетевые теоремы.
Системные напряжения и токи можно найти, подробно нарисовав схему и используя законы Кирхгофа и другие сетевые теоремы.
Эффективность и реактивная мощность 
 Обратите внимание также на примеры в конце описания калькулятора.
Обратите внимание также на примеры в конце описания калькулятора. Для расчёта мощности и нагрузки по известным напряжению и току выберите тип соединения (звезда или треугольник) и введите напряжение (линейное ИЛИ фазное), ток (линейный ИЛИ фазный) и коэффициент мощности. Нажмите на кнопку Рассчитать. Мощность и параметры нагрузки будут рассчитаны автоматически. Также можно, рассчитать мощность и ток по известным напряжению и нагрузке. Для этого выберите тип соединения (звезда ИЛИ треугольник) и введите напряжение (линейное ИЛИ фазное) и импеданс нагрузки в каждой фазе в комплексной ИЛИ полярной форме. Нажмите на кнопку Рассчитать. Калькулятор автоматически рассчитает мощность и ток.
Для расчёта мощности и нагрузки по известным напряжению и току выберите тип соединения (звезда или треугольник) и введите напряжение (линейное ИЛИ фазное), ток (линейный ИЛИ фазный) и коэффициент мощности. Нажмите на кнопку Рассчитать. Мощность и параметры нагрузки будут рассчитаны автоматически. Также можно, рассчитать мощность и ток по известным напряжению и нагрузке. Для этого выберите тип соединения (звезда ИЛИ треугольник) и введите напряжение (линейное ИЛИ фазное) и импеданс нагрузки в каждой фазе в комплексной ИЛИ полярной форме. Нажмите на кнопку Рассчитать. Калькулятор автоматически рассчитает мощность и ток. Расчет мощности и тока по заданным напряжению и нагрузке
Расчет мощности и тока по заданным напряжению и нагрузке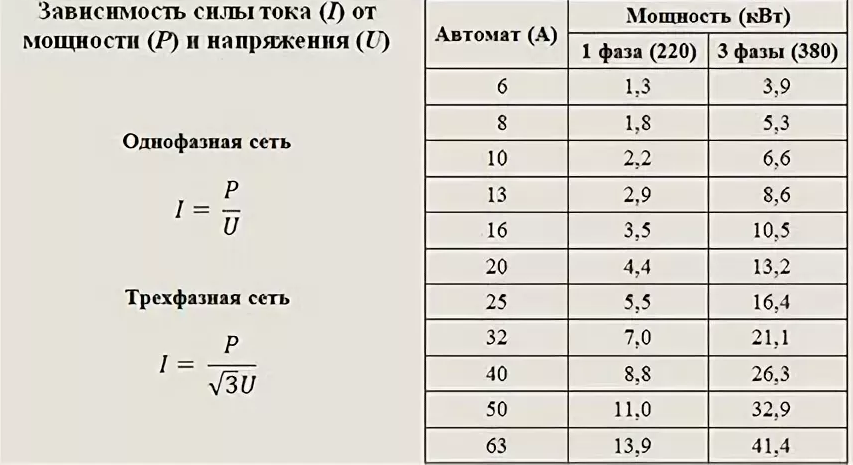 Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети.
Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети. Однофазная система не годится для питания мощных электродвигателей.
Однофазная система не годится для питания мощных электродвигателей. В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
 Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.
Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.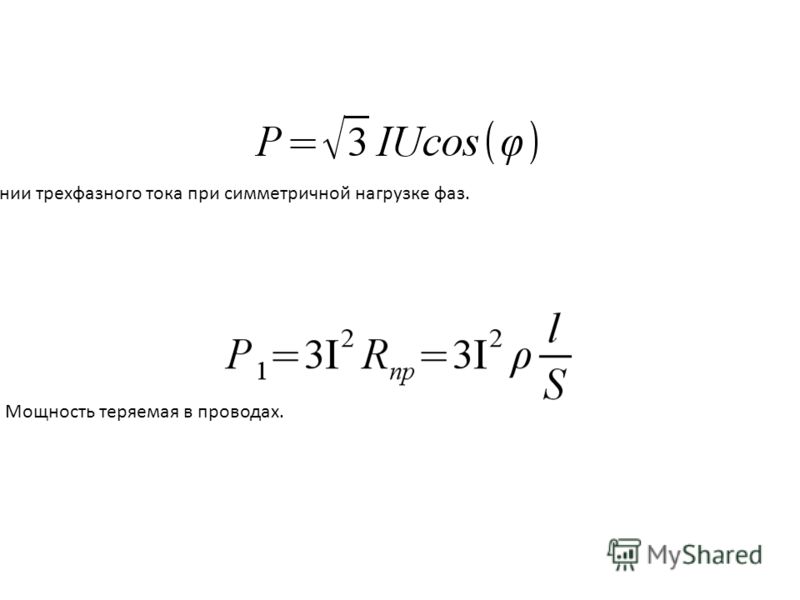 Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю:
Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю: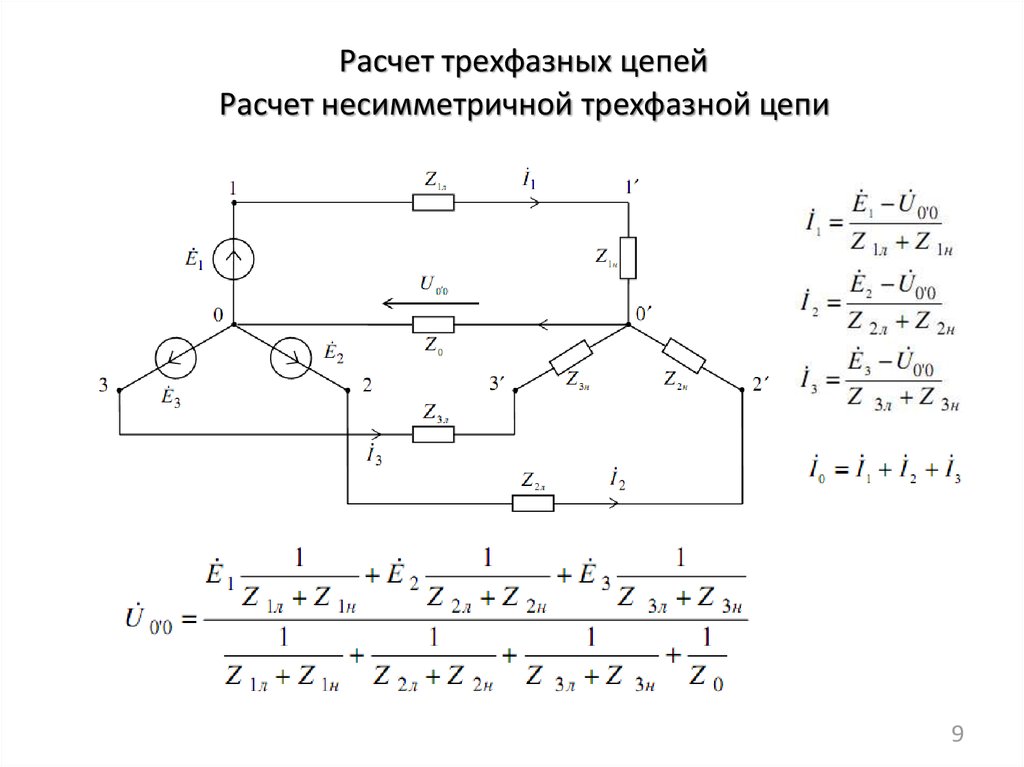 Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ.
Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ. В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна
В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать
Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать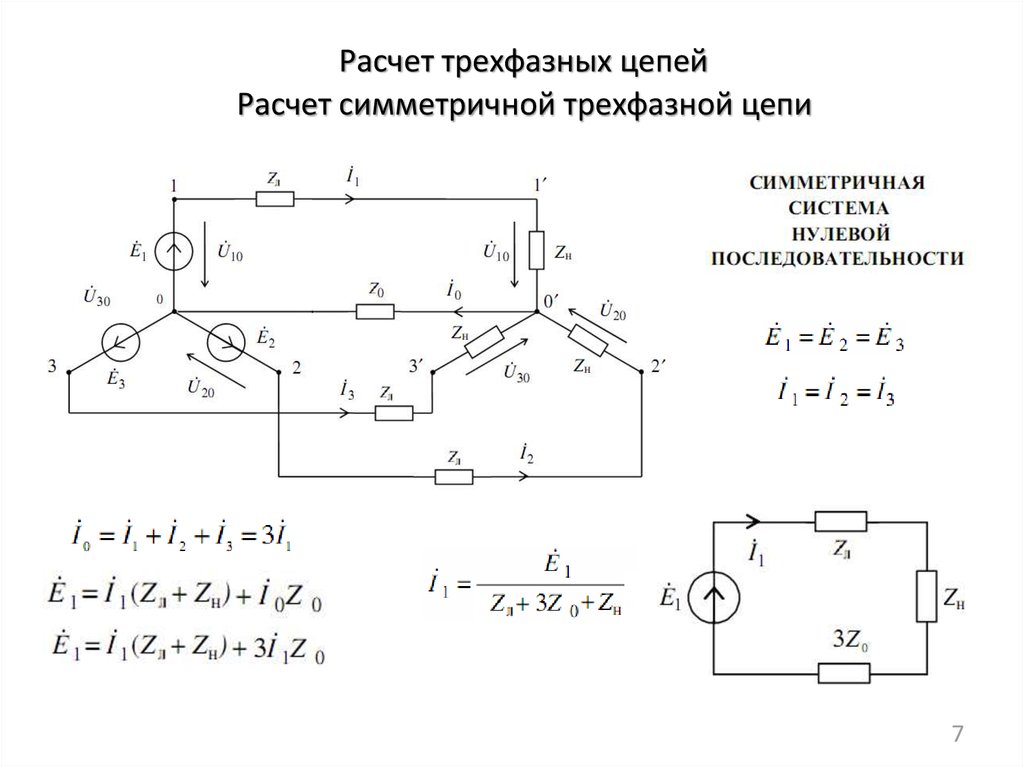 Мы используем их в этом калькуляторе.
Мы используем их в этом калькуляторе. Полная мощность также уменьшилась:
Полная мощность также уменьшилась:
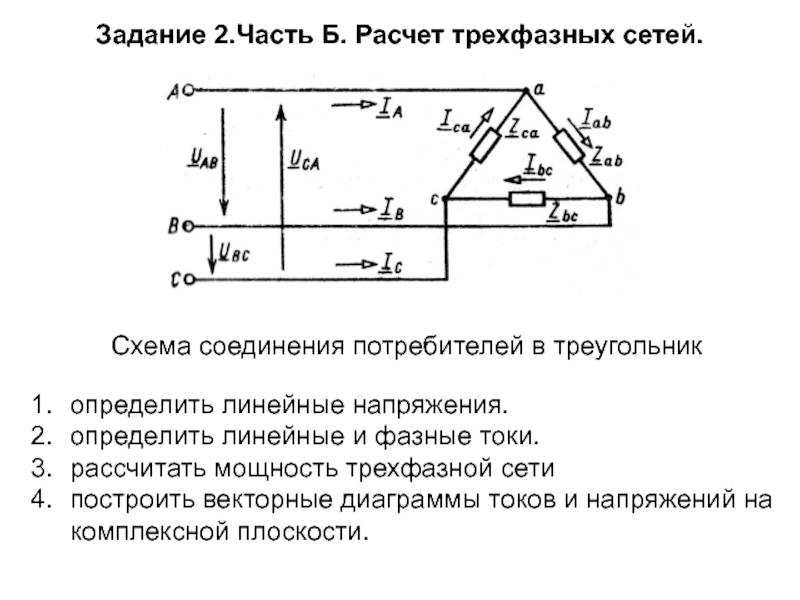
 Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке.
Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке.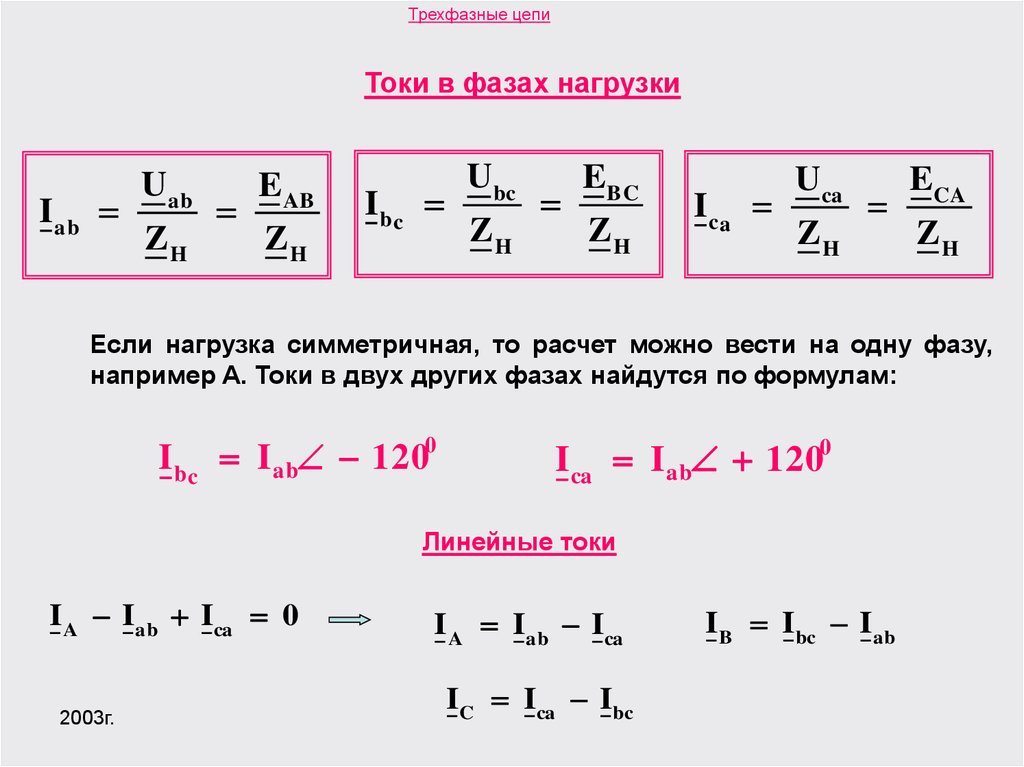 Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор.
Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор. В каждом фазном проводе протекает ток Iph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности.
В каждом фазном проводе протекает ток Iph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов т.ВН – 6 кВ;
т.ВН – 6 кВ;
 Конечно, если у вас есть какие-то сверхспособности к запоминанию формулы, вы всегда можете придерживаться этого подхода.
Конечно, если у вас есть какие-то сверхспособности к запоминанию формулы, вы всегда можете придерживаться этого подхода.