Как сделать красивые снежинки из бумаги
13 декабря 2022 Ликбез Сделай сам
Плоские и объёмные фигуры, которыми можно украсить окно или комнату к Новому году.
Как вырезать плоские снежинки из бумаги
Как сложить бумагу
Есть несколько способов это сделать. Во всех случаях у вас получится шестиугольная снежинка. Так что выбирайте тот вариант, который вам больше нравится.
Вариант 1
Вырежьте из бумаги квадрат. Чтобы сделать его из листа формата А4, загните одну короткую сторону к длинной и отрежьте получившийся сбоку прямоугольник.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeСогните квадрат по диагонали. Затем сложите фигуру пополам, соединяя два противоположных острых угла. Не сгибайте бумагу полностью, а лишь наметьте место сгиба внизу.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeРазогните фигуру. Загните одну сторону наверх так, чтобы нижний угол получившего треугольника был на отметке.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeДругую часть загните точно так же, но на обратную сторону. Верхние боковые треугольники должны быть одинаковыми, поэтому при необходимости подровняйте фигуру.
Верхние боковые треугольники должны быть одинаковыми, поэтому при необходимости подровняйте фигуру.
Если не получается сложить углы ровно, сделайте карандашную разметку, как показано здесь:
С обратной стороны наложите правую часть фигуры на левую, сложив её пополам.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeПереверните фигуру — вы увидите ровный прямой край. Разрежьте по нему бумагу. Можно для удобства обвести этот край карандашом.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeВот видеоинструкция:
Вариант 2
Вырежьте из бумаги квадрат. Сложите его по диагонали.
Кадр: СreativeClub / YouTubeЗатем согните треугольник пополам.
Кадр: СreativeClub / YouTubeПолучившуюся фигуру поместите прямым углом вверх, а сгибом — влево. Загните правую сторону чуть дальше середины треугольника.
Кадр: СreativeClub / YouTubeЛевую сторону сложите внахлёст на правую. Загнутые треугольники должны получиться одинаковыми.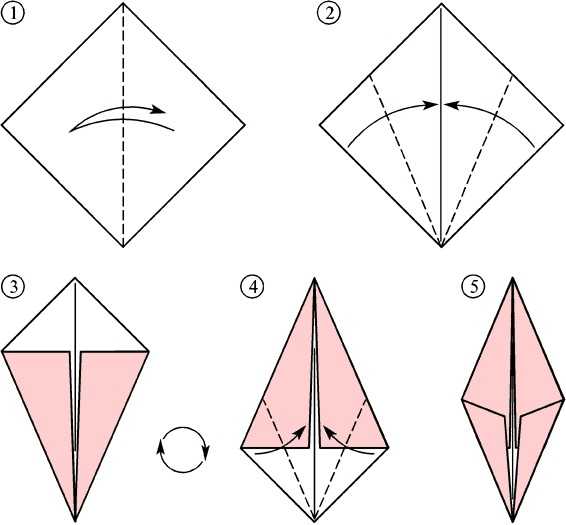
С обратной стороны отрежьте бумагу по линии, как и в предыдущем варианте.
Кадр: СreativeClub / YouTubeНаглядный процесс:
Как нарисовать узор
На получившемся треугольнике нужно нарисовать лишь половину одной вершины снежинки. Помните: середина этой вершины располагается на сгибе бумажной заготовки.
Нарисуйте узор карандашом. Не нажимайте на него слишком сильно.
Кадр: Amazing Easy Origami — Yakomoga / YouTubeУзор можно придумать самому или воспользоваться готовыми шаблонами из интернета. На самом деле узоров снежинок очень много и рисунок может быть любым, ведь всё зависит от фантазии рисующего. Так что не бойтесь её проявить.
Как вырезать снежинку
Разрежьте бумагу по нарисованным линиям. Там, где узор мелкий, удобнее воспользоваться маленькими маникюрными ножницами.
Затем аккуратно расправьте бумагу.
Если вам не нравятся сгибы на снежинке, накройте её тканью или пергаментом и прогладьте утюгом.
Как сделать объёмные снежинки из бумаги
Все плоские снежинки вырезаются по одному принципу, а вот способы смастерить объёмные фигуры отличаются друг от друга.
Например, для такого пушистого украшения нужно вырезать несколько одинаковых снежинок разного размера и приклеить друг на друга:
Для этой снежинки одинаковые резные детали нужно склеить по кругу:
Похожий вариант:
Эта снежинка делается очень просто, но выглядит потрясающе:
Чтобы собрать такую снежинку, понадобится шаблон. Распечатайте его, вырежьте детали и склейте, как показано в видео:
С помощью этого мастер‑класса вы создадите большую ажурную снежинку из шести одинаковый деталей:
youtube.com/embed/lT2oeNkTOAk» frameborder=»0″ allowfullscreen=»allowfullscreen»>Для этого похожего украшения тоже понадобятся шесть бумажных квадратов, но детали склеиваются иначе:
Здесь показано, как склеить снежинку из отдельных бумажных полосок:
А вот другой вариант зимней фигуры из полос бумаги:
Читайте также 🎄⛄️🎁
- Как эффектно упаковать подарок любой формы и размера
- 20 милых снеговиков своими руками
- 8 по-настоящему новогодних причёсок для девочек
- 20 снежных фигур, которые легко сделать самому и с детьми
- 50 крутых ёлочных игрушек своими руками
*Деятельность Meta Platforms Inc. и принадлежащих ей социальных сетей Facebook и Instagram запрещена на территории РФ.
и принадлежащих ей социальных сетей Facebook и Instagram запрещена на территории РФ.
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Содержание
- Как сделать куб из бумаги?
- Как сделать конус из бумаги?
- Как сделать цилиндр из бумаги?
- Как сделать параллелепипед из бумаги?
- Как сделать пирамиду из бумаги?
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.

- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра.
 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания.

- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
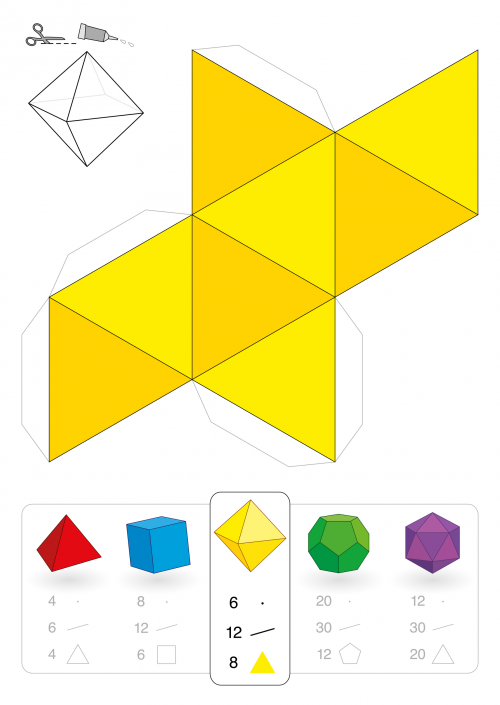
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.

- Вырезаем и склеиваем фигуру.
- Пирамида готова!
- фигуры из бумаги
- пирамида
- куб
- цилиндр
- параллелепипед
Читайте также:
Определение, типы, свойства, формы, примеры
Параллелограмм — это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны.
На данном рисунке изображен параллелограмм ABCD, у которого AB II CD и AD II BC. Кроме того, AD = BC и AB = CD.
Когда мы смотрим вокруг себя, мы видим множество параллелограммообразных форм и объектов в виде зданий, плиток или бумаги.
Здания : Многие здания построены в форме параллелограмма. Знаменитой реальной иллюстрацией является офисное здание Dockland в Гамбурге, Германия.
Плитка : Плитка бывает разных форм и размеров. Одной из наиболее часто встречающихся форм плитки является параллелограмм.
Ластик : Всем знаком классический ластик. Ластики тоже бывают разных форм и размеров, один из них имеет форму параллелограмма. Грани этого ластика имеют форму параллелограмма.
Ластики тоже бывают разных форм и размеров, один из них имеет форму параллелограмма. Грани этого ластика имеют форму параллелограмма.
Площадь параллелограмма определяется по формуле A = bh , где b — длина основания, а «h» — высота.
Периметр параллелограмма равен сумме длин четырех сторон. Поскольку противоположные стороны параллелограмма равны, его периметр также может быть выражен как удвоенная сумма смежных сторон, т. е. 2 (AB + BC)
SplashLearn преобразует образование для детей начальной школы от детского сада до 5 класса. SplashLearn мотивирует детей изучать математику с помощью увлекательных и персонализированных программ. Доступный на всех цифровых платформах, он был использован более чем 40 миллионами детей по всему миру. Чтобы узнать больше о параллелограммах, нажмите здесь.
На рисунке ниже ABCD представляет собой параллелограмм, где ∠DAB = 75° и ∠CBD = 60°. Вычислите ∠BDC.
Как известно, противоположные углы параллелограмма равны.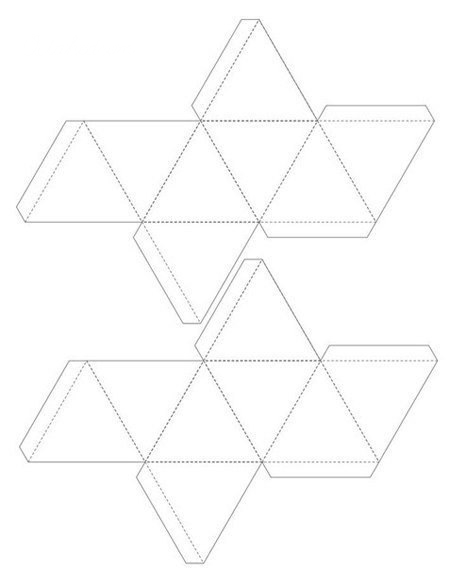 Следовательно, ∠DCB = ∠DAB = 75°.
Следовательно, ∠DCB = ∠DAB = 75°.
Найдите площадь этого параллелограмма с основанием 15 см и высотой 6 см.
1 Каков периметр параллелограмма ABCD, две смежные стороны которого равны 12 м и 8 м соответственно?40 м 20 м 4 м 30 м Правильный ответ: 40 м 2 90 040 Что из перечисленного не является параллелограммом?Прямоугольник Ромб Квадрат Трапеция Правильный ответ: Трапеция 3 В параллелограмме ABCD, если ∠A = 60°, то ∠D равно140° 130° 120° 110° Правильный ответ: 120° |
Является трапецией параллелограмм?
Нет, трапеция не является параллелограммом, потому что у параллелограмма две пары параллельных сторон, а у трапеции только одна пара параллельных сторон.
Все ли прямоугольники параллелограммы?
Да, все прямоугольники являются параллелограммами, потому что прямоугольник имеет два набора параллельных сторон и две пары противоположных сторон, которые равны. Следовательно, он соблюдает все свойства параллелограмма.
Все ли параллелограммы прямоугольники?
Нет, параллелограмм не всегда является прямоугольником. В прямоугольнике все углы должны быть равны 90°. Но для параллелограмма никакие углы не должны быть равны 90°.
Всегда ли диагонали параллелограмма делят друг друга пополам?
Да, диагонали параллелограмма всегда делят друг друга пополам.
Нужно ли, чтобы в четырехугольнике все стороны были равны, чтобы он был параллелограммом?
Нет, у параллелограмма не все стороны равны. Только противоположные стороны параллелограмма равны.
Вопрос Видео: Нахождение периметра ромба
Стенограмма видео
Определите периметр ромба 𝐴𝐵𝐶𝐷, учитывая, что точки 𝐴 и 𝐵 равны минус пять, минус один и минус четыре, четыре.
Начнем с того, что вспомним, что этот ромб является четырехугольником, все четыре стороны которого равны. Ромб здесь 𝐴𝐵𝐶𝐷, но нам даны только две точки и нам нужно найти периметр всего ромба. Итак, давайте возьмем бумагу с сеткой и посмотрим, сможем ли мы нанести эти две точки 𝐴 и 𝐵. Итак, здесь у нас есть точки 𝐴 при минус пяти, минус один и 𝐵 при минус четыре, четыре. Мы даже можем соединить их, чтобы создать отрезок 𝐴𝐵.
Итак, как нам найти периметр? Ведь ромб 𝐴𝐵𝐶𝐷 мог выглядеть так, а мог выглядеть вот так. Но давайте задумаемся на минуту. Мы можем помнить, что периметр фигуры — это расстояние вокруг внешнего края.
Это можно сделать двумя способами. Мы могли бы использовать теорему Пифагора или эту формулу, чтобы найти расстояние между двумя точками, что на самом деле является применением теоремы Пифагора. Эта формула говорит нам, что для двух точек 𝑥 один, 𝑦 один и 𝑥 два, 𝑦 два, расстояние рассчитывается как квадратный корень из 𝑥 двух минус 𝑥 один в квадрате плюс 𝑦 два минус 𝑦 один в квадрате. Итак, давайте воспользуемся этой формулой, и мы сможем показать, что на самом деле нам даже не нужно было рисовать сетку с 𝐴 и 𝐵 на ней. Возьмем формулу и обозначим точку 𝐴 со значениями 𝑥 один, 𝑦 один и точку 𝐵 со значениями 𝑥 два, 𝑦 два.
Таким образом, мы получили бы расстояние, равное квадратному корню из 𝑥 двух, что равно отрицательному четырем, вычесть 𝑥 единицу, что составляет минус пять, все в квадрате плюс четыре, это было наше значение 𝑦 два, вычесть отрицательную единицу, что является нашим 𝑦 одно значение в квадрате.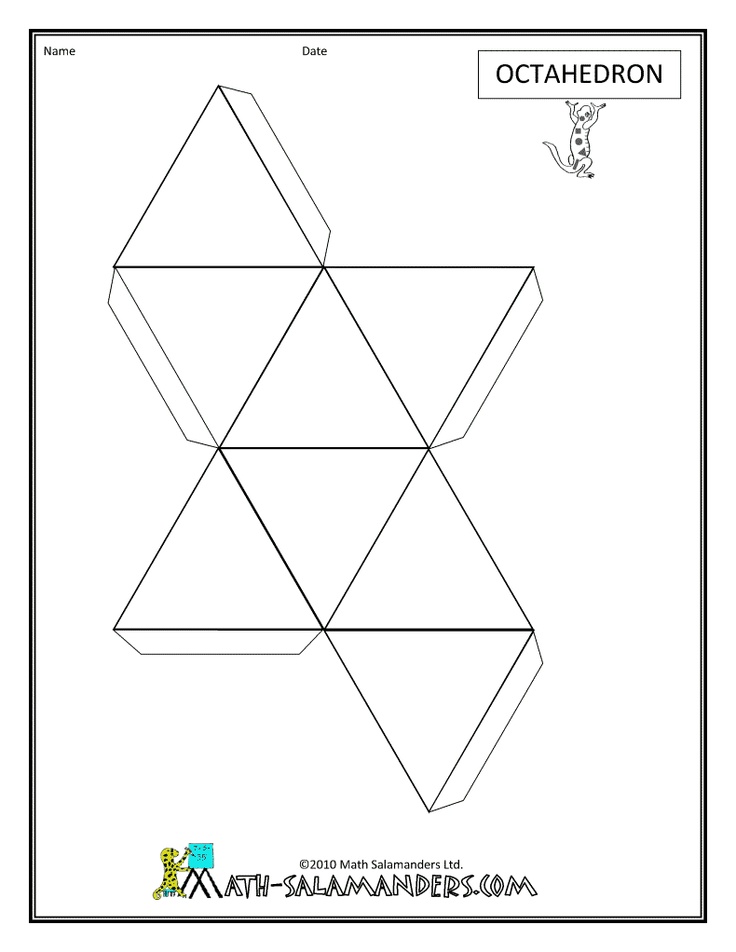
Здесь также следует добавить единицы измерения. Мы проработали дистанцию. Итак, это будет единица длины. Итак, теперь мы знаем, что у нас есть длина 𝐴𝐵. Это квадратный корень из 26 единиц длины. И мы сохраним его в форме квадратного корня, пока продолжаем вычислять периметр. Помните, что не имеет значения, как выглядит 𝐴𝐵𝐶𝐷. Мы знаем, что длина одной стороны будет равна квадратному корню из 26. Поскольку у ромба четыре стороны одинаковой длины, периметр будет в четыре раза больше корня 26. И мы можем записать это просто как четыре корня из 26 единиц длины. И это наш ответ для периметра ромба 𝐴𝐵𝐶𝐷.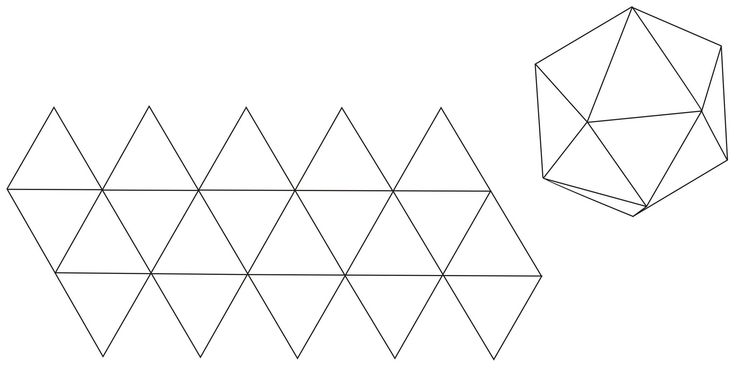
 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
 Итак, ∠A = ∠C = 60°, а также ∠B = ∠D
Итак, ∠A = ∠C = 60°, а также ∠B = ∠D